Gaussian curve fitting in physics-CodePudding

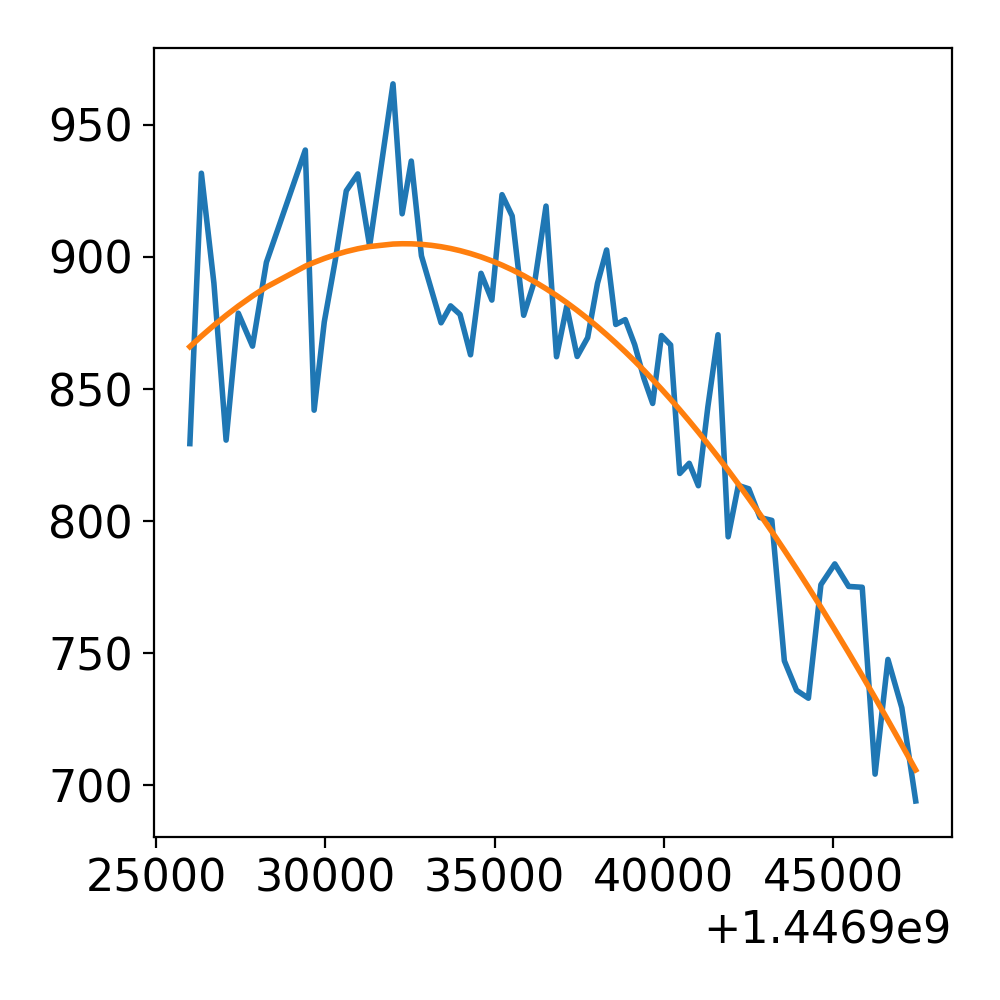
I have this data, I tried to fit by a Gaussian function but I can't found an appropriate function, I tried using curve_fit from scipy.optimize :

time_s = [1.44692600e 09, 1.44692634e 09, 1.44692671e 09, 1.44692707e 09,
 1.44692743e 09, 1.44692785e 09, 1.44692826e 09, 1.44692941e 09,
 1.44692967e 09, 1.44692997e 09, 1.44693029e 09, 1.44693062e 09,
 1.44693096e 09, 1.44693131e 09, 1.44693200e 09, 1.44693227e 09,
 1.44693254e 09, 1.44693284e 09, 1.44693313e 09, 1.44693342e 09,
 1.44693370e 09, 1.44693398e 09, 1.44693429e 09, 1.44693460e 09,
 1.44693492e 09, 1.44693522e 09, 1.44693552e 09, 1.44693586e 09,
 1.44693620e 09, 1.44693652e 09, 1.44693683e 09, 1.44693713e 09,
 1.44693744e 09, 1.44693775e 09, 1.44693804e 09, 1.44693831e 09,
 1.44693858e 09, 1.44693886e 09, 1.44693914e 09, 1.44693941e 09,
 1.44693967e 09, 1.44693993e 09, 1.44694020e 09, 1.44694047e 09,
 1.44694075e 09, 1.44694102e 09, 1.44694130e 09, 1.44694160e 09,
 1.44694190e 09, 1.44694220e 09, 1.44694251e 09, 1.44694284e 09,
 1.44694319e 09, 1.44694356e 09, 1.44694392e 09, 1.44694427e 09,
 1.44694464e 09, 1.44694505e 09, 1.44694546e 09, 1.44694586e 09,
 1.44694624e 09, 1.44694662e 09, 1.44694703e 09, 1.44694744e 09]

Temperature = [829.331306, 931.702088, 890.075633, 830.659093, 878.715978, 866.238768
, 897.958014, 940.495055, 841.990924, 875.391469, 898.393043, 925.048353
, 931.445104, 904.151363, 965.550728, 916.348809, 936.315168, 900.445995
, 887.76832,  875.064126, 881.480871, 878.240278, 862.958271, 893.813659
, 883.678318, 923.593998, 915.52458,  877.919073, 891.754242, 919.274917
, 862.223914, 881.275387, 862.33147,  869.461632, 890.014577, 902.656117
, 874.446393, 876.284046, 866.751916, 854.095049, 844.540741, 870.263794
, 866.687327, 818.019291, 821.875267, 813.385138, 843.198211, 870.558259
, 794.039978, 813.497634, 812.217789, 801.361143, 800.263045, 747.101493
, 735.923635, 732.930255, 775.930026, 783.786631, 775.255742, 774.938671
, 704.186773, 747.612911, 729.315237, 694.021293]

I used this code :

def Gauss(x, a1, b1, c1, a2, b2, c2 ):
    return a1*np.exp(-((x-b1)/c1)**2)   a2*np.exp(-((x-b2)/c2)**2)
parameters, covariance = curve_fit(Gauss, time_s, Temperature)
plt.plot(time_s, Gauss(time_s, *parameters))
plt.show()

this is the result of this fit :

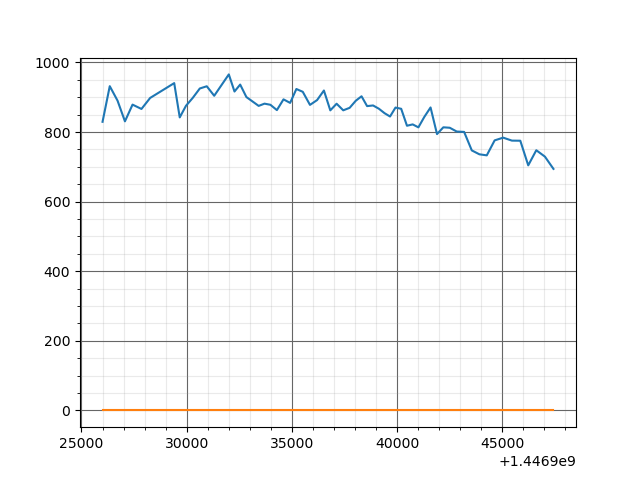
Very bad fit

The error message :

/home/lhoussine/anaconda3/lib/python3.8/site-packages/scipy/optimize/minpack.py:828: OptimizeWarning: Covariance of the parameters could not be estimated
  warnings.warn('Covariance of the parameters could not be estimated',

CodePudding user response：

First, you're not fitting a Gaussian function, you're fitting the sum of a couple of functions. I'm not sure why, but it certainly doesn't help and doesn't match your question.

But even if we fit a single Gaussian, the main problem is the initial guess for curve_fit. Unless you say otherwise,