All combinations of all elements of a 2D array-CodePudding

So I have matrix A

A = [[0,0,1,-1] 
     [0,0,1,-1]
     [0,0,1,-1]
     [0,0,1,-1]]

And I want to have all the possible combinations with these elements. This means that rows can change between them and columns as well. In this situation, I would expect a 4^4 = 256 possibilities. I have tried:

combs = np.array(list(itertools.product(*A)))

It does creates me, my desire to output a matrix of (256,4), but all the rows are equal. This means that I get vector [0,0,1,-1], 256 times.

Here is an example:

output = [[0,0,0,0]
          [0,0,0,1]
          [0,0,1,1]
          [0,1,1,1]
          [1,1,1,1]
          [-1,1,1,-1]
          [-1,-1,-1,-1]
             ....
          [0,-1,0,-1]

Another example, if

A = [[1,2,3] 
     [4,5,6]
     [7,8,9]]

The output should be all the possible combinations of arrays that the matrix can form

Combs =[[1,1,1] 
        [1,1,2]
        [1,1,3]
        [1,1,...9]
        [2,1,1]
        [2,2,1]
        [1,2,1]

Another example would be: I have the vector layers

layers = [1,2,3,4,5]

And then I have vector angle

angle = [0,90,45,-45]

each layer can have one of the angles, so I create a matrix A

A = [[0,90,45,-45]
     [0,90,45,-45]
     [0,90,45,-45]
     [0,90,45,-45]
     [0,90,45,-45]]

Great, but now I want to know all possible combinations that layers can have. For example, layer 1 can have an angle of 0º, layer 2 an angle of 90º, layer 3 an angle of 0º, layer 4 an angle of 45º and layer 5 and an angle of 0º. This creates the array

Comb = [0,90,0,45,0]

So all the combinations would be in a matrix

Comb = [[0,0,0,0,0]
        [0,0,0,0,90]
        [0,0,0,90,90]
        [0,0,90,90,90] 
        [0,90,90,90,90] 
        [90,90,90,90,90] 
             ...
        [0,45,45,45,45]
        [0,45,90,-45,90]]

How can I generalize this process for bigger matrices.

Am I doing something wrong?

Thank you!

CodePudding user response：

It's OK to use np.array in conjunction with list(iterable), especially in your case where iterable is itertools.product(*A). However, this can be optimised since you know the shape of array of your output.

There are many ways to perform product so I'll just put my list:

Methods of Cartesian Product

import itertools
import numpy as np

def numpy_product_itertools(arr):
    return np.array(list(itertools.product(*arr)))

def numpy_product_fromiter(arr):
    dt = np.dtype([('', np.intp)]*len(arr)) #or np.dtype(','.join('i'*len(arr)))
    indices = np.fromiter(itertools.product(*arr), dt)
    return indices.view(np.intp).reshape(-1, len(arr))

def numpy_product_meshgrid(arr):
    return np.stack(np.meshgrid(*arr), axis=-1).reshape(-1, len(arr))

def numpy_product_broadcast(arr): #a little bit different type of output
    items = [np.array(item) for item in arr]
    idx = np.where(np.eye(len(arr)), Ellipsis, None)
    out = [x[tuple(i)] for x,i in zip(items, idx)]
    return list(np.broadcast(*out))

Example of usage

A = [[1,2,3], [4,5], [7]]
numpy_product_itertools(A)
numpy_product_fromiter(A)
numpy_product_meshgrid(A)
numpy_product_broadcast(A)

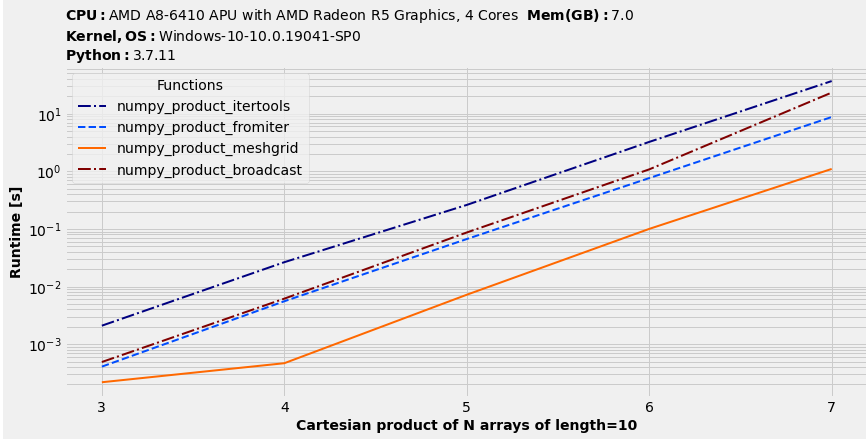
Comparison of performance

import benchit
benchit.setparams(rep=1)
%matplotlib inline
sizes = [3,4,5,6,7]
N = sizes[-1]
arr = [np.arange(0,100,10).tolist()] * N
fns = [numpy_product_itertools, numpy_product_fromiter, numpy_product_meshgrid, numpy_product_broadcast]
in_ = {s: (arr[:s],) for s in sizes}
t = benchit.timings(fns, in_, multivar=True, input_name='Cartesian product of N arrays of length=10')
t.plot(logx=False, figsize=(12, 6), fontsize=14)

Note that numba beats majority of these algorithms although it's not included.