Python Multiply Matrix by Vector of Matrices-CodePudding

Does anybody know of a way (preferably using numpy or something similar) to multiply a matrix by a vector of matrices and obtain the desired product shown below? Basically the idea is to follow the normal rules of matrix multplication of a matrix and a vector, only the elements of the vector are matrices themselves and not numbers.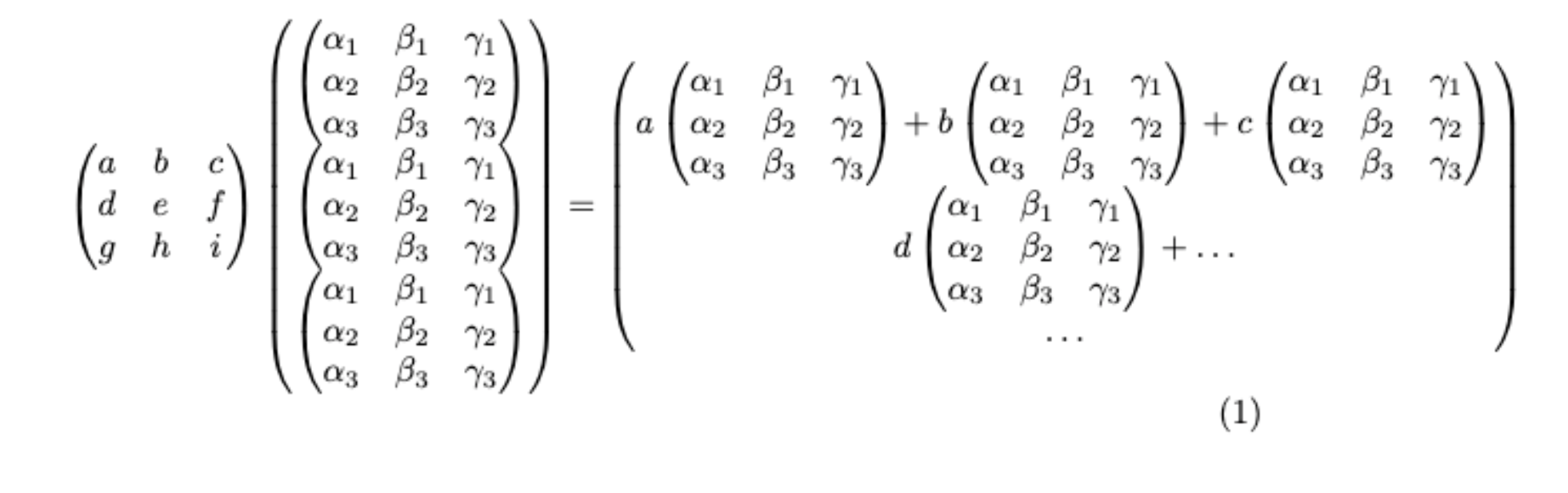

CodePudding user response：

If I understand the question correctly, you can try this:

import numpy as np

A = np.arange(3*3*3).reshape(3, 3, 3)
b = np.arange(9).reshape(3, 3)
print(f"A=\n{A}\n\nb=\n{b}")

It gives:

A=
[[[ 0  1  2]
  [ 3  4  5]
  [ 6  7  8]]

 [[ 9 10 11]
  [12 13 14]
  [15 16 17]]

 [[18 19 20]
  [21 22 23]
  [24 25 26]]]

b=
[[0 1 2]
 [3 4 5]
 [6 7 8]]

Then:

out = ([email protected](2, 0, 1)).transpose(1, 2, 0)
print(out)

which gives:

[[[ 45  48  51]
  [ 54  57  60]
  [ 63  66  69]]

 [[126 138 150]
  [162 174 186]
  [198 210 222]]

 [[207 228 249]
  [270 291 312]
  [333 354 375]]]

The matrix out[0] is equal to 0*A[0] 1*A[1] 2*A[2], out[1] is equal to 3*A[0] 4*A[1] 5*A[2] etc.

CodePudding user response：

Is this what you want to calculate:

# Define two matrices
A = np.arange(9).reshape(3, 3)
B = np.arange(9, 18).reshape(3, 3)

# First calculate the desired result:
rows = []
for i in range(3):
    rows.append([A[i, j] * B for j in range(3)])
result = np.stack(rows).sum(axis=1)
assert(result.shape == (3, 3, 3))
print(result)

[[[ 27  30  33]
  [ 36  39  42]
  [ 45  48  51]]

 [[108 120 132]
  [144 156 168]
  [180 192 204]]

 [[189 210 231]
  [252 273 294]
  [315 336 357]]]

Is this correct?

If so, then here is the same calculation using numpy's einsum function:

C = np.array([B] * 3)  # shape (3, 3, 3)
result = np.einsum("ij,jkl->ikl", A, C)