Reconstructing Markov chain from figure in R-CodePudding

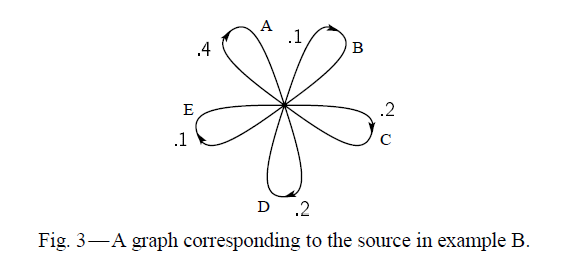
I am trying to reconstruct a Markov process from Shannons paper "A mathematical theory of communication". My question concerns figure 3 on page 8 and a corresponding sequence (message) from that Markov chain from page 5 section (B). I just wanted to check if I coded the right Markov chain to this figure from Shannons paper:

Here is my attempt:

install.packages("markovchain")
library(markovchain)

MessageABCDE = c("A", "B", "C", "D", "E")

MessageTransitionMatrix = matrix(c(.4,.1,.2,.2,.1,
                                   .4,.1,.2,.2,.1,
                                   .4,.1,.2,.2,.1,
                                   .4,.1,.2,.2,.1,
                                   .4,.1,.2,.2,.1),
                                 nrow = 5,
                                 byrow = TRUE,
                                 dimname = list(MessageABCDE, MessageABCDE))

MCmessage = new("markovchain", states = MessageABCDE,
                byrow = TRUE,
                transitionMatrix = MessageTransitionMatrix,
                name = "WritingMessage") 


steadyStates(MCmessage)

markovchainSequence(n = 20, markovchain = MCmessage, t0 = "A")

My goal was to also create a sequence (message) from that chain. I am mostly uncertain about the transition matrix, where infered the probabilities had to be all the same in every row. I am happy with the output of markovchainSequence, but I am not 100% sure, if I am doing it right.

Here is my console output for markovchainSequence:

> markovchainSequence(n = 20, markovchain = MCmessage, t0 = "A")
 [1] "D" "E" "A" "D" "A" "A" "B" "D" "E" "C" "A" "A" "E" "C" "C" "D" "D" "D"
[19] "A" "C"

CodePudding user response：

Looks fine. It's maybe odd because with fully independent states like this there isn't any need for a Markov chain. One could equally well use

tokens <- c("A", "B", "C", "D", "E")
probs  <- c(0.4, 0.1, 0.2, 0.2, 0.1)

sample(tokens, size=20, replace=TRUE, prob=probs)
## [1] "A" "B" "A" "B" "D" "B" "C" "D" "A" "D" "C" "E" "A" "A" "C" "E" "C" "D" "C" "C"

Will likely make more sense once there is a variety of conditional probabilities.