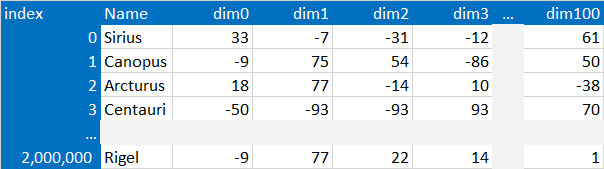
- I have a Pandas DataFrame of 2 million entries
- Each entry is a point in a 100 dimensional space
- I want to compute the Euclidian distance between the N last points and all the others to find the closest neighbors (to simplify let's say find the top#1 closest neighbor for the 5 last points)
- I have done the code below for a small dataset, but it's fairly slow, and I'm looking for ideas of improvement (especially speed improvement!)
The logic is the following:
- Split the dataframe between target for which we want to find the closest neighbor and compare : all others among which we will look for the neighbor
- Iterate through the targets
- Compute the Squared Euclidean distance of each df_compare point VS the target
- Select the top#1 value of the compare df and save its ID in the target dataframe
import pandas as pd
import numpy as np
data = {'Name': ['Ly','Gr','Er','Ca','Cy','Sc','Cr','Cn','Le','Cs','An','Ta','Sa','Ly','Az','Sx','Ud','Lr','Si','Au','Co','Ck','Mj','wa'],
'dim0': [33,-9,18,-50,39,-23,-19,89,-74,81,8,23,-63,-62,-14,45,39,-46,74,19,7,97,-29,71,],
'dim1': [-7,75,77,-93,-89,4,-96,-64,41,-27,-87,23,-69,-77,-92,18,21,27,-76,-57,-44,20,15,-76,],
'dim2': [-31,54,-14,-93,72,-14,65,44,-88,19,48,-51,-25,36,-46,98,8,0,53,-47,-29,95,65,-3,],
'dim3': [-12,-86,10,93,-79,-55,-6,-79,-12,66,-81,-14,44,84,9,-19,-69,29,-50,-59,35,-28,90,-73,],
}
df = pd.DataFrame(data)
df_target = df.tail(5)
df_target['closest_neighbour'] = np.nan
df_compare= df.drop(df.tail(5).index)
for i, target_row in df_target.iterrows():
df_compare['distance'] = 0
for dim in df_target.columns:
if dim.startswith('dim'):
df_compare['distance'] = df_compare['distance'] (target_row[dim] - df_compare[dim])**2
df_compare.sort_values(by=['distance'], ascending=True, inplace=True)
closest_neighbor=df_compare.head(1)
df_target.loc[df_target.index==i,'closest_neighbour']= closest_neighbor['Name'].iloc[0]
print(df_target)
Any suggestion of improvement of the logic or the code is welcome! Cheers
CodePudding user response:
Constructing the dataframe with drop_duplicates('Name') because I find that at least Ly appears twice.
import pandas as pd
import numpy as np
data = {'Name': ['Ly','Gr','Er','Ca','Cy','Sc','Cr','Cn','Le','Cs','An','Ta','Sa','Ly','Az','Sx','Ud','Lr','Si','Au','Co','Ck','Mj','wa'],
'dim0': [33,-9,18,-50,39,-23,-19,89,-74,81,8,23,-63,-62,-14,45,39,-46,74,19,7,97,-29,71,],
'dim1': [-7,75,77,-93,-89,4,-96,-64,41,-27,-87,23,-69,-77,-92,18,21,27,-76,-57,-44,20,15,-76,],
'dim2': [-31,54,-14,-93,72,-14,65,44,-88,19,48,-51,-25,36,-46,98,8,0,53,-47,-29,95,65,-3,],
'dim3': [-12,-86,10,93,-79,-55,-6,-79,-12,66,-81,-14,44,84,9,-19,-69,29,-50,-59,35,-28,90,-73,],
}
df = pd.DataFrame(data).drop_duplicates('Name')
df_target = df.tail(5)
df_compare= df.drop(df.tail(5).index)
One way is to apply a row-wise operation
df_target = df_target.set_index('Name')
df_compare = df_compare.set_index('Name')
df_compare.apply(lambda r: ((r - df_target)**2).sum(axis=1), axis=1).idxmin()
Outcome:
Name
Au Ly
Co Az
Ck Sx
Mj Lr
wa Cn
dtype: object
Another, which is my preference, is to do it in numpy array:
pd.DataFrame(
((df_target.values[:, np.newaxis] - df_compare.values)**2).sum(axis=2),
columns = df_compare.index,
index = df_target.index,
).idxmin(axis=1)
which will yield the same outcome
CodePudding user response:
If you get numpy arrays out of the data frame, you can compute them using Numba fast:
from timeit import default_timer as timer
from numba import jit
import math
import numpy as np
data = {'Name': [""]*1000,
'dim0': [0]*1000,
'dim1': [0]*1000,
'dim2': [0]*1000,
'dim3': [0]*1000,
}
# add rest of dims
for i in range(96):
data["dim" str(i 4)]=[0]*1000
dims=len(data)-1
N=len(data["Name"])
print(dims)
print(N)
def distance(selected,selected2):
dif=selected-selected2
dif*=dif
dist=0.0
for val in dif:
dist = val
return math.sqrt(dist)
@jit(nopython=True)
def distanceNumba(selected,selected2):
dif=selected-selected2
dif*=dif
dist=0.0
for val in dif:
dist = val
return math.sqrt(dist)
cache=[];
for i in range(N):
cache.append(np.zeros(dims))
cache=np.asarray(cache)
for i in range(dims):
for j in range(N):
cache[j][i]=data["dim" str(i)][j]
selected=cache[0]
out = np.zeros(N)
def distances(selected,cache,out):
i=0
for selected2 in cache:
out[i]=distance(selected,selected2)
i=i 1
@jit(nopython=True)
def distancesNumba(selected,cache,out):
i=0
for selected2 in cache:
out[i]=distanceNumba(selected,selected2)
i=i 1
for i in range(10):
t1 = timer()
distances(selected,cache,out)
t2 = timer()
print(t2-t1," seconds without numba")
t1 = timer()
distancesNumba(selected,cache,out)
t2 = timer()
print(t2-t1," seconds with numba")
print(out)
output:
100
1000
0.05954742600079044 seconds without numba
1.2770428250005352 seconds with numba
0.0608673019996786 seconds without numba
0.0009444430033909157 seconds with numba
0.060780961997807026 seconds without numba
0.0009288470027968287 seconds with numba
0.06079873300041072 seconds without numba
0.0009262589992431458 seconds with numba
0.06075674100065953 seconds without numba
0.0009228080016328022 seconds with numba
0.06063023499882547 seconds without numba
0.0009203600020555314 seconds with numba
0.0607308569997258 seconds without numba
0.0009688009995443281 seconds with numba
0.06056219499805593 seconds without numba
0.000959154000156559 seconds with numba
0.060522257001139224 seconds without numba
0.0009322579971922096 seconds with numba
0.06055161300173495 seconds without numba
0.000933799001359148 seconds with numba
If you have CUDA graphics card, then you can use it too:
from timeit import default_timer as timer
from numba import jit
from numba import cuda
import numba
import math
import numpy as np
data = {'Name': [""]*1000,
'dim0': [0]*1000,
'dim1': [0]*1000,
'dim2': [0]*1000,
'dim3': [0]*1000,
}
# add rest of dims
for i in range(96):
data["dim" str(i 4)]=[0]*1000
dims=len(data)-1
N=len(data["Name"])
print(dims)
print(N)
def distance(selected,selected2):
dif=selected-selected2
dif*=dif
dist=0.0
for val in dif:
dist = val
return math.sqrt(dist)
cache=[];
for i in range(N):
cache.append(np.zeros(dims))
cache=np.asarray(cache,dtype=np.float32)
for i in range(dims):
for j in range(N):
cache[j][i]=data["dim" str(i)][j]
selected=cache[0]
out = np.zeros(N)
def distances(selected,cache,out):
i=0
for selected2 in cache:
out[i]=distance(selected,selected2)
i=i 1
@cuda.jit
def distancesNumba(selected,cache,out):
i=0
for selected2 in cache:
dif=cuda.local.array(shape=dims, dtype=numba.float32)
dif[cuda.threadIdx.x]=selected[cuda.threadIdx.x]-selected2[cuda.threadIdx.x]
dif[cuda.threadIdx.x]*=dif[cuda.threadIdx.x]
dist=0.0
numba.cuda.syncthreads()
if cuda.threadIdx.x==0:
for j in range(dims):
dist = dif[j]
out[i]=math.sqrt(dist)
i=i 1
for i in range(10):
t1 = timer()
distances(selected,cache,out)
t2 = timer()
print(t2-t1," seconds without numba")
t1 = timer()
# 1=blocks, 100=threads
distancesNumba[1,100](selected,cache,out)
t2 = timer()
print(t2-t1," seconds with numba")
print(out)
output:
100
1000
0.09203408300163574 seconds without numba
1.3188036539977475 seconds with numba
0.09138548299961258 seconds without numba
0.00905935400078306 seconds with numba
0.09278915700269863 seconds without numba
0.011017041997547494 seconds with numba
0.09266194800147787 seconds without numba
0.009332213001471246 seconds with numba
0.09425603599811438 seconds without numba
0.008965768000052776 seconds with numba
0.09545346899903961 seconds without numba
0.009094572000321932 seconds with numba
0.09400588900098228 seconds without numba
0.008994818999781273 seconds with numba
0.09595919099956518 seconds without numba
0.009412939001776977 seconds with numba
0.09670166400246671 seconds without numba
0.009072380998986773 seconds with numba
0.09463289600171265 seconds without numba
0.009022546000778675 seconds with numba
this performance is only by 100 CUDA threads and without reduction optimization for the distance (simply adds 100 values by 1 cuda thread after the squared differences are computed). You can adjust number of threads for kernel, optimize with reduction for distance summation and get higher performance.
Then you can simply sort the "out" array to get the shortest/longest distances.
Edit: optimization for more CUDA threads (1 block per line, dims threads per block) reduction in kernel
@cuda.jit
def distancesNumba(selected,cache,out):
i=0
selected2=cuda.blockIdx.x
dif=cuda.local.array(shape=dims, dtype=numba.float32)
dif[cuda.threadIdx.x]=selected[cuda.threadIdx.x]-cache[selected2][cuda.threadIdx.x]
dif[cuda.threadIdx.x]*=dif[cuda.threadIdx.x]
dist=0.0
numba.cuda.syncthreads()
reduction=128
while reduction>0:
if reduction cuda.threadIdx.x < dims:
dif[reduction] = dif[reduction cuda.threadIdx.x]
numba.cuda.syncthreads()
reduction>>=2
if cuda.threadIdx.x==0:
out[selected2]=math.sqrt(dif[0])
and launching it with:
# compute distances of selected line to N lines (dims dimensional)
distancesNumba[N,dims](selected,cache,out)
performance becomes:
100 <-- dimensions
100000 <-- N
8.610873253001046 seconds without numba
1.8519197440000426 seconds with numba
8.927837033999822 seconds without numba
0.20861789699847577 seconds with numba
8.859914688000572 seconds without numba
0.20821334699940053 seconds with numba
8.980341544000112 seconds without numba
0.21734917999856407 seconds with numba
8.818792854999629 seconds without numba
0.22718691900081467 seconds with numba
9.003342153999256 seconds without numba
0.2289118230000895 seconds with numba
9.02532176999739 seconds without numba
0.20479743699979736 seconds with numba
8.9248614370008 seconds without numba
0.21945642799983034 seconds with numba
For 1 million lines and 100 dimensions:
100
1000000
81.72404483399805 seconds without numba
8.821669873999781 seconds with numba
86.97093956900062 seconds without numba
2.0208445850003045 seconds with numba
84.32691005200104 seconds without numba
2.0129999929995392 seconds with numba
it's only 40x performance because it is making only single distance check against all lines. Adding 4-5 more distances to check per line would be more efficient. You can also do "tiling" optimization to use L1 cache of GPU for even higher performance.
CodePudding user response:
Your dataframe stores the columns as numpy arrays. But for your calculations, it would probably be more efficient to have the dimn rows as numpy arrays, because the distance calculation could then leverage numpy array operations.
CodePudding user response:
More Effienet Algorithm
Rather than using Brute Force, you can use Tree Methods
Advantages of Tree Methods (e.g. BallTree, KDTree, etc.)
For N points in Target and Compare
- Brute Force complexity is N*N
- Tree Methods complexity is N*log(N)
- This makes Tree methods significant faster than Brute Force for large N (e.g. 2M)
Code
import pandas as pd
import numpy as np
from sklearn.neighbors import BallTree
# Data
df_target = df.tail(5)
df_compare= df.drop(df.tail(5).index)
# Create Distance Tree with Euclidean distance metric (skipping Name column)
tree = BallTree(df_compare[df_compare.columns[1:]].values, metric = "euclidean")
# Find nearest neighbor for each node in target (skipping Name column)
distances, indices = tree.query(df_target[df_target.columns[1:]].values, k = 1)
# Show closest name in compare for each name in target
for target, compare in zip(df_target['Name'], df_compare.iloc[indices.flatten()]['Name']):
print(f"{target} {compare}")
Output
Au Ly
Co Az
Ck Sx
Mj Lr
wa Cn