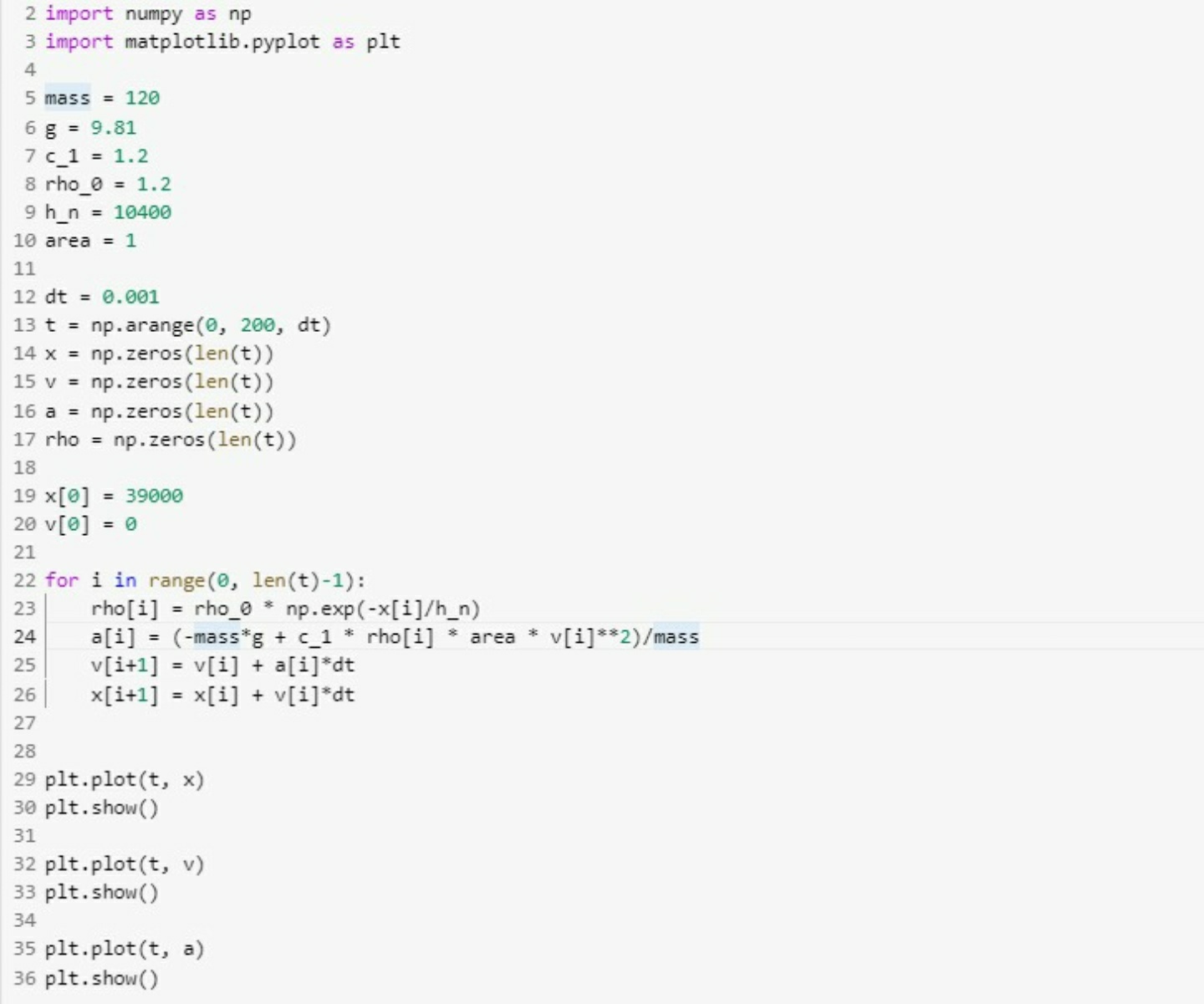
I have to model an object that is in free fall with air resistance. Above are pictures with the code and of the graphs.

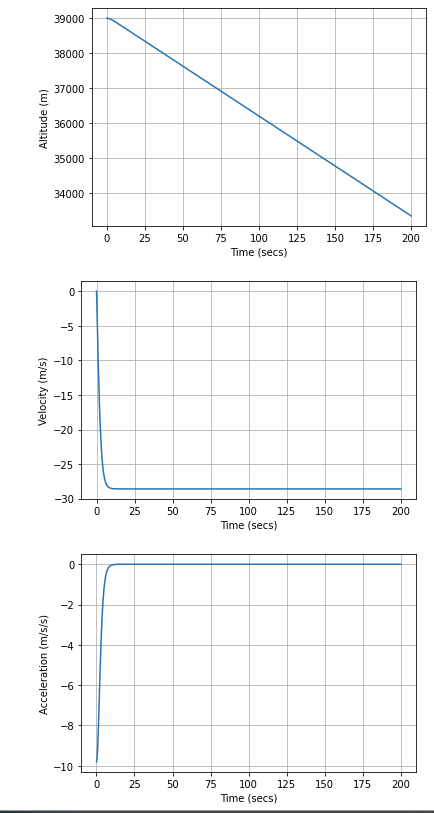
Top graph: x (position) against t (time) Middle graph: v (speed) against t Bottom graph: a (acceleration) against t

Problems:

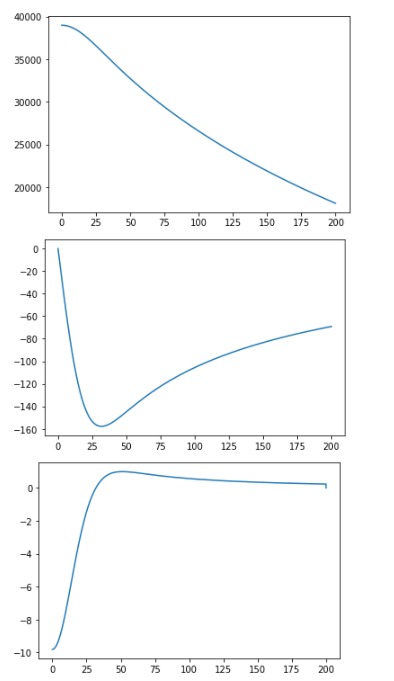
• The velocity keeps increasing pretty fast even though the acceleration is roughly 0. The velocity should eventually become constant since acceleration will eventually be 0 and stay zero since the gravitational force is equal to the drag force.
• The acceleration becomes rougly 0 eventually but it is not exactly 0, even though mathematically it should become 0 and stay 0 once the two forces are equal to each other.
• You would expect the height to decrease much faster. From these outputs, you are still at 20000 m after 200s.

I can't figure out why the velocity doesn't eventually stay constant and how the acceleration can exceed 0?

Here are relevant equations that I have used:

Note: I used Newtons second law to find the expression for the acceleration (line 24)

Fnet = ma = -mg C * rho * A * v^2

CodePudding user response：

The acceleration becomes rougly 0 eventually but it is not exactly 0, even though mathematically it should become 0 and stay 0 once the two forces are equal to each other.

Mathematically, the force of drag becomes arbitrarily close to the force of gravity, but is never exactly equal. This is a consequence of differential equations, which you should look up but can be explored in part