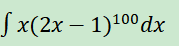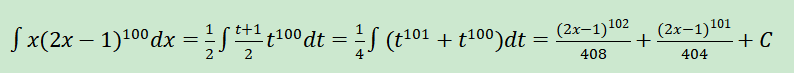Sympy integration with high order expressions; integral transform-CodePudding

I'm using Anaconda python 3.8.5 and sympy 1.9 to integrate

whereas clearly this integration can be solved as:

But I tried integrate(x * (2 * x - 1) ** 100, x)

and sympy gives me result as:

(with more lines not shown).

Is there any way that I can get the correct results? Thanks.

CodePudding user response：

The result shown is correct although expanded. You can verify that by differentiating and factoring:

In [36]: integrate(x*(2*x - 1)**100, x).diff(x).factor()
Out[36]: 
           100
x⋅(2⋅x - 1)

You can use a manual substitution to get it in the form that you asked for:

In [34]: Integral(x*(2*x - 1)**100, x).transform(2*x-1, t).doit().subs(t, 2*x-1)
Out[34]: 
         102            101
(2⋅x - 1)      (2⋅x - 1)   
────────────   ────────────
    408            404

Note that the constant of integration is implicit.