How to tweak my code to get this smoother/fatter distance map using cv2.distanceTransform?-CodePudding

I was reading a paper that used distance transform to get a probability map, as shown below: 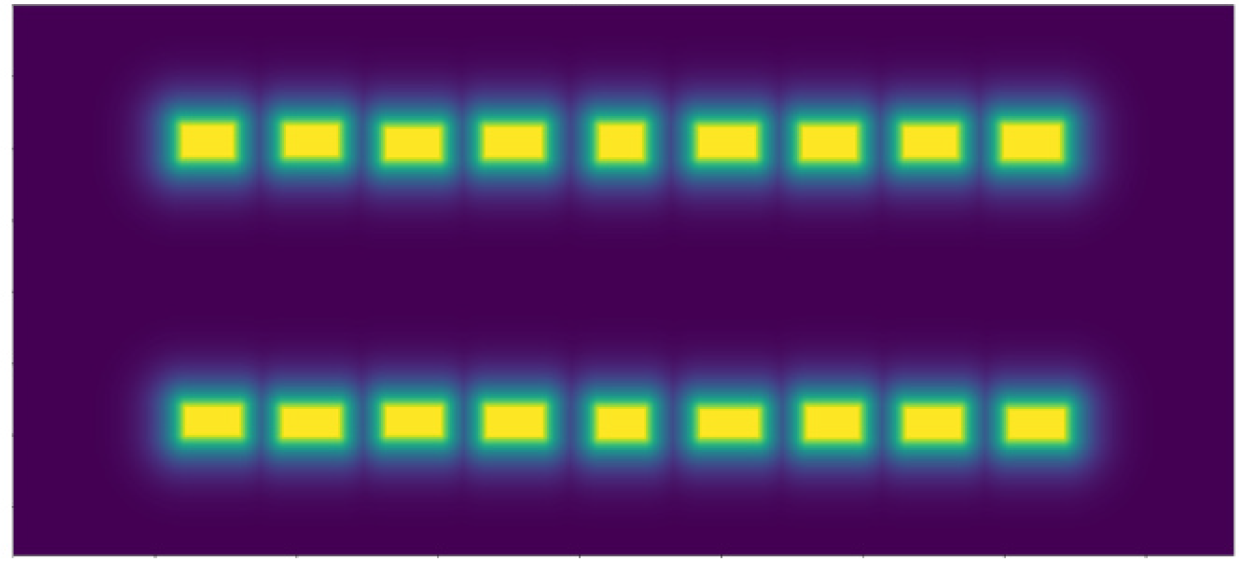using the binary image: The map by the paper is so much more "concentrated and filled" (notice the fatter yellow and no pointy lines), compared to mine:

According to the paper, this is what it's described as:

...convert them to continuous distance maps by a distance transform and normalize them from 0 to 1 to form a probability map

This is my code:

import numpy as np
import matplotlib.pyplot as plt
import cv2

m = np.zeros((720, 1280), dtype=np.uint8)
pts = np.array([[320, 360], [640, 360], [960, 360]])
# rectangle size
rh, rw = 100, 120

for x, y in pts:
    m = cv2.rectangle(m, (int(x - rw / 2), int(y - rh / 2)), (int(x   rw / 2), int(y   rh / 2)), (255, 255, 255), -1)
m = cv2.distanceTransform(m, cv2.DIST_L2, cv2.DIST_MASK_5)
plt.imshow(m)

Any idea how to tweak my code to get closer to what the paper did?

CodePudding user response：

You need to first invert your image m, so that your boxes become black. Then perform distance threshold:

inv_m = cv2.bitwise_not(m)
dist_img = cv2.distanceTransform(inv_m, cv2.DIST_L2, 3)
norm_img = cv2.normalize(dist_img, dist_img, 0, 1.0, cv2.NORM_MINMAX)

Using scikit image library, scale the range of intensity to 255:

scale_img = skimage.exposure.rescale_intensity(norm_img, in_range='image', out_range=(0,255)).astype(np.uint8)

Now create a range within this intensity scale, here I chose input range of (0-30). And then invert it:

scale_img2 = skimage.exposure.rescale_intensity(scale_img, in_range=(0,30), out_range=(0,255)).astype(np.uint8)
final_img = cv2.bitwise_not(scale_img2)

This post is based on a recent answer by fmw42