Why does triangle expands when i rotate it?-CodePudding

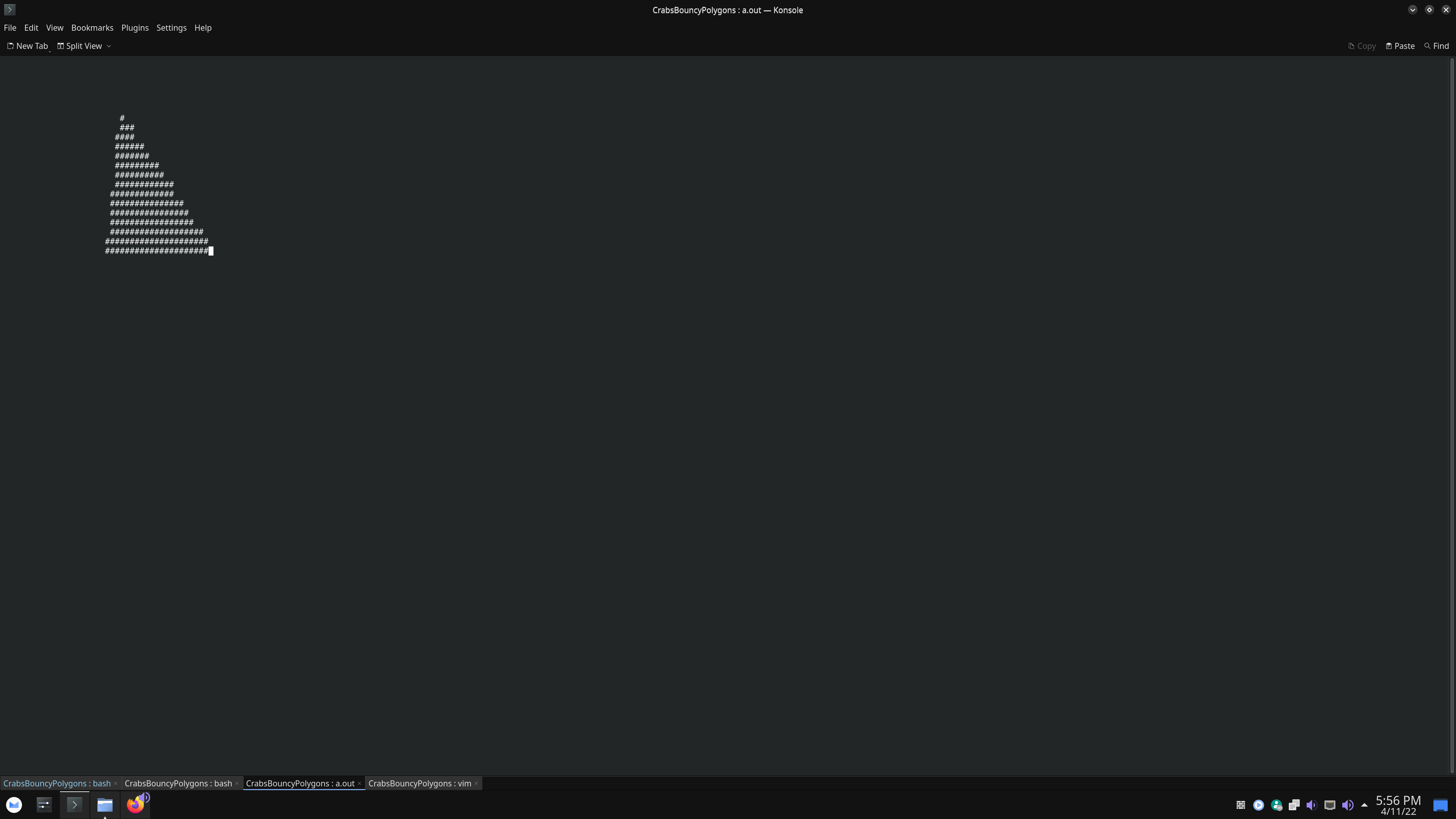
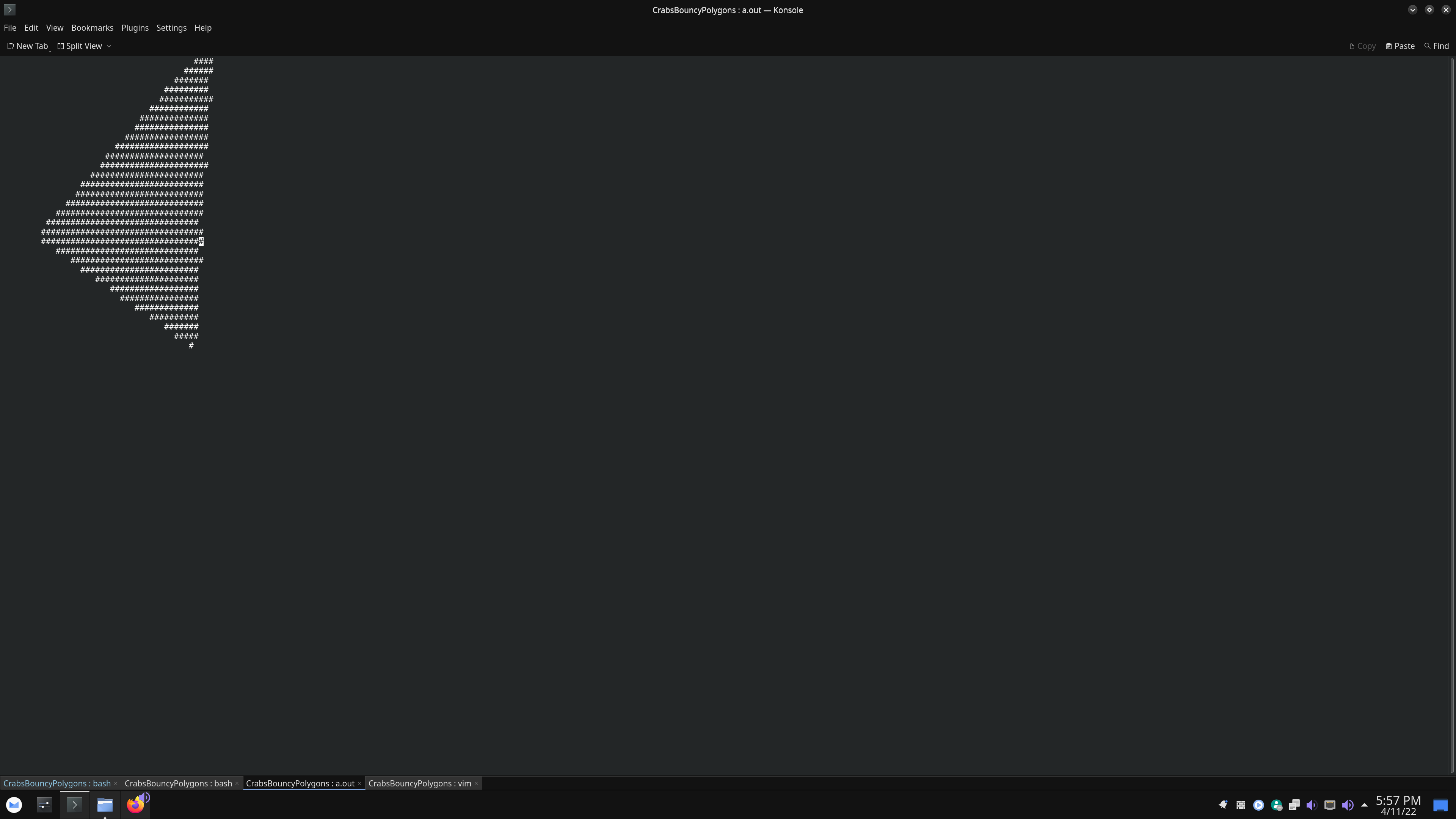
I've been trying to make a collision simulation in c with ncurses but there is one major problem. It seems that my triangle expands with rotational motion and I don't know what's causing it. It also doesn't expand when I comment out the updateTri() function but then it also doesn't rotate.

#include<stdlib.h>
#include<stdio.h>
#include<curses.h>
#include<math.h>
#include<time.h>
#include<sys/ioctl.h>
#include<sys/time.h>
#include<unistd.h>
    
struct winsize win;
    
typedef struct vector2d{
    double x;
    double y;
} Vec2;
    
typedef struct triangle{
    Vec2 *p1;
    Vec2 *p2;
    Vec2 *p3;
}Tri;
    
//
//DRAWING STUFF
//
    
void swapp(Vec2 *p1,Vec2 *p2){Vec2 tmp = *p1;*p1 = *p2;*p2 = tmp;}
    
double inpolx(Vec2 p1,Vec2 p2,double y){ //interpolate x from p1 to p2 with y variable
    double x = p1.x   (p2.x - p1.x)*(y - p1.y)/(p2.y - p1.y);
    return x;
}
    
void DSline(double x1,double x2,double y ){ //Draws Simple line
        
    double x,x2l;
    if(x1<x2){
        x=x1;x2l = x2;
    }else{
        x=x2;x2l = x1;
    }
    do{mvprintw(y/2,x,"#");
    } while(x  <x2l);
}
    
void drawtup(Tri t){
    Vec2 *p1 = t.p1,*p2 = t.p2,*p3 = t.p3;
    double invslope1 = (p2->x - p1->x) / (p2->y - p1->y),invslope2 = (p3->x - p1->x) / (p3->y - p1->y),curx1 = p1->x,curx2 = p1->x;
    for(double Y = p1->y; Y < p2->y; Y  ){
        DSline(curx1,curx2,Y);
        curx1  = invslope1;
        curx2  = invslope2;
    }
}

void drawtdown(Tri t){
    Vec2 *p1 = t.p1,*p2 = t.p2,*p3 = t.p3;
    double invslope1 = (p3->x - p1->x) / (p3->y - p1->y),invslope2 = (p3->x - p2->x) / (p3->y - p2->y),curx1 = p3->x,curx2 = p3->x;
    for(double Y = p3->y; Y > p1->y; Y--){
        DSline(curx1,curx2,Y);
        curx1 -= invslope1;
        curx2 -= invslope2;
    }
}
    
void scanln(Tri tr){
    if(tr.p2->y < tr.p1->y){ swapp(tr.p2, tr.p1); }if(tr.p3->y <tr.p1->y){ swapp(tr.p3, tr.p1); }if(tr.p3->y < tr.p2->y){ swapp(tr.p3, tr.p2); }
    
    if(tr.p3->y == tr.p2->y){
        drawtup(tr);
    }
    else if(tr.p1->y == tr.p2->y){
        drawtdown(tr);
    }
    else{
        Vec2 p4 = {inpolx(*tr.p1,*tr.p3,tr.p2->y),tr.p2->y};
        Tri tu = {tr.p1,tr.p2,&p4};
        Tri td = {tr.p2,&p4,tr.p3};
        drawtup(tu);
        drawtdown(td);
    }
}
    
//
//SIMULATION CALCULATIONS
//
    
Vec2 crossd(Vec2 p ,double d){
    Vec2 r = {-1*d*p.y,d*p.x};
    return r;
}

Vec2 addVec(Vec2 p,Vec2 offs){
    Vec2 v;
    v.x =p.x  offs.x;
    v.y =p.y  offs.y;
    return v;
}

Vec2 mulv(Vec2 p,double u){
    Vec2 pr = {p.x*u,p.y*u};
    return pr;
}
    
void moveVec(Vec2 *v,Vec2 offs){ //brooom
    v->x  = offs.x;
    v->y  = offs.y;
}
        
Vec2 cenTri(Tri t){
    Vec2 v ={(t.p1->x t.p2->x t.p3->x)/3,(t.p1->y t.p2->y t.p3->y)/3};
    return v;
}

void updateTri(Tri *t,Vec2 v,double w){
    Vec2 cen = cenTri(*t);
    Vec2 r1 = {t->p1->x-cen.x,t->p1->y-cen.y};
    moveVec(t->p1,addVec(v,crossd(r1,w)));
    
    Vec2 r2 = {t->p2->x-cen.x,t->p2->y-cen.y};
    moveVec(t->p2,addVec(v,crossd(r2,w)));
    
    Vec2 r3 = {t->p3->x-cen.x,t->p3->y-cen.y};
    moveVec(t->p3,addVec(v,crossd(r3,w)));
}
    
int main(){
    int ms = 10;
    ioctl(STDOUT_FILENO, TIOCGWINSZ, &win);
    time_t start, now, s_T, e_T;struct timespec delay;delay.tv_sec = 0;delay.tv_nsec = ms * 999999L;time(&start);
        
    initscr();
    clear();
    Vec2 p[3] = {{20,26},{22,45},{46,25}};Tri t = {&p[0],&p[1],&p[2]};
    
    
    double mass = 100;
    Vec2 v = {0,0};
    double w = 0.2;
    
    while(1){
        ioctl(STDOUT_FILENO, TIOCGWINSZ, &win);
        Vec2 screen = {win.ws_col,win.ws_row};
    
        nanosleep(&delay,NULL);

        updateTri(&t,v,w);
        clear();
        scanln(t);
        refresh();
    }
    getch();
    return 0;
}

Triangle at t

Triangle at t x

CodePudding user response：

The problem is

void updateTri(Tri *t,Vec2 v,double w){
    Vec2 cen = cenTri(*t);
    Vec2 r1 = {t->p1->x-cen.x,t->p1->y-cen.y};
    moveVec(t->p1,addVec(v,crossd(r1,w)));
    
    Vec2 r2 = {t->p2->x-cen.x,t->p2->y-cen.y};
    moveVec(t->p2,addVec(v,crossd(r2,w)));
    
    Vec2 r3 = {t->p3->x-cen.x,t->p3->y-cen.y};
    moveVec(t->p3,addVec(v,crossd(r3,w)));
}

which updates the verticles according to the instantaneous velocity of the vertex has over a finite amount of time (which is arbitrarily chosen as timeStep = 1 here ).

At any instant in time the velocity of a vertex r_i located relative to the rotation center is

v_i = ω × r_i

but at the next instant in time the position of the particle is

r_i^* = r_i δt * v_i

so the new velocity should be

v_i = ω × r_i^*

and so forth when δt → 0.

But for a finite time step, you cannot do the above, because it is always going to move the points in a straight line for each step δt. So you always going to have distortion.

What you need to do is consider the location of each vertex considering the overall rotation angle of the body

p1->x = cen->x   a*cos(θ) - b*sin(θ);
p1->y = cen->y   a*sin(θ)   b*cos(θ);

where a and b are constants describing the location of the vertex in the body frame (with zero rotation).

Summary Only rotations can preserve lengths, and so the kinematics of the problem (the quantities to describe all possible configurations and motions) need to include the orientation angle for each body, and the positions/velocties etc to be derived from this angle.

CodePudding user response：

These modifications to the code will preserve the size and shape of the triangle:

// return vector p rotated by angle d
Vec2 crossd(Vec2 p ,double d){
    double s = sin(d);
    double c = cos(d);
    Vec2 r = { c*p.x - s*p.y, s*p.x   c*p.y };
    return r;
}

void updateTri(Tri *t,Vec2 v,double w){
    Vec2 cen = cenTri(*t);
    v = addVec(v,cen);

    Vec2 r1 = {t->p1->x-cen.x,t->p1->y-cen.y};
    *t->p1 = addVec(v,crossd(r1,w));
    
    Vec2 r2 = {t->p2->x-cen.x,t->p2->y-cen.y};
    *t->p2 = addVec(v,crossd(r2,w));
    
    Vec2 r3 = {t->p3->x-cen.x,t->p3->y-cen.y};
    *t->p3 = addVec(v,crossd(r3,w));
}