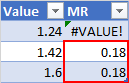
I am trying to compare two cells in a table:
The column "MR" is calculated using the formula =ABS([@Value]-A1) to determine the moving range of the column "Value". The values in the "Value" column are not rounded. The highlighted cells in the "MR" column (B3 and B4) are equal. I can enter the formula =B3=B4 into a cell and Excel says that B3 is equal to B4.
But when I compare them in VBA, VBA says that B4 is greater than B3. I can select cell B3 and enter the following into the Immediate Window ? selection.value = selection.offset(1).value. That statement evaluates to false.
I tried removing the absolute value from the formula thinking that might have had something to do with it, but VBA still says they aren't equal.
I tried adding another row where Value=1.78 so MR=0.18. Interestingly, the MR in the new row (B5) is equal to B3, but is not equal to B4.
I then tried increasing the decimal of A4 to match the other values, and now VBA says they are equal. But when I added the absolute value back into the formula, VBA again says they are not equal. I removed the absolute value again and now VBA is saying they are not equal.
Why is VBA telling me the cells are not equal when Excel says they are? How can I reliably handle this situation through VBA going forward?
CodePudding user response:
The problem is that the IEEE 754 Standard for Floating-Point Arithmetic is imprecise by design. Virtually every programming language suffers because of this.
IEEE 754 is an extremely complex topic and when you study it for months and you believe you understand fully, you are simply fooling yourself!
Accurate floating point value comparisons are difficult and error prone. Think long and hard before attempting to compare floating point numbers!
The Excel program gets around the issue by cheating on the application side. VBA on the other hand follows the IEEE 754 spec for Double Precision (binary64) faithfully.
A Double value is represented in memory using 64 bits. These 64 bits are split into three distinct fields that are used in binary scientific notation:
- The SIGN bit (1 bit to represent the sign of the value: pos/neg)
- The EXPONENT (11 bits, biased in value by 1023)
- The MANTISSA (53 bits, 52 bits stored 1 bit implied)
The math works like this: Stored Value = SIGN VALUE * 2^UNBIASED EXPONENT * MANTISSA
Note that a value of 1 in the sign bit denotes a negative SIGN VALUE while a 0 denotes a positive SIGN VALUE.
The problem always boils down to the same thing.
The vast majority of real numbers cannot be expressed precisely within this system which introduces small rounding errors that propagate like weeds.
With your example numbers...
1.24 is represented with the following binary:
Sign bit = 0
Exponent = 01111111111
Mantissa = 0011110101110000101000111101011100001010001111010111
The Hex pattern over the full 64 bits is precisely: 3FF3D70A3D70A3D7.
The precision is derived exclusively from the 53-bit mantissa and the exact decimal value from the binary is: 0.2399999999999999911182158029987476766109466552734375
In this instance the value of "1" is implied and so the complete decimal value is exactly:
1.2399999999999999911182158029987476766109466552734375
Now notice that this is not precisely 1.24 and that is the entire problem.
Let's examine 1.42:
Sign bit = 0
Exponent = 01111111111
Mantissa = 0110101110000101000111101011100001010001111010111000
The Hex pattern over the full 64 bits is precisely: 3FF6B851EB851EB8.
With the implied "1" the complete decimal value is stored as:
1.4199999999999999289457264239899814128875732421875000
And again not precisely 1.42
Now, let's examine 1.6:
Sign bit = 0
Exponent = 01111111111
Mantissa = 1001100110011001100110011001100110011001100110011010
The Hex pattern over the full 64 bits is precisely: 3FF999999999999A.
Notice the repeating binary fraction in this case that is truncated when the mantissa bits run out? Obviously this can never be precisely accurate in the same way as 1/3 can never be accurately represented in decimal base10.
With the implied "1" the complete decimal value is stored as:
1.6000000000000000888178419700125232338905334472656250
Not exactly 1.6, but closer than the others!
Now let's subtract the full stored double precision representations:
1.60 - 1.42 = 0.18000000000000015987
1.42 - 1.24 = 0.17999999999999993782
So as you can see, they are not equal at all.
The usual way to work around this is threshold testing, basically an inspection to see if two values are close enough... and that depends on you and your requirements. Be forewarned, effective threshold testing is way harder than it appears at first glance.
@chris neilsen linked to an interesting Microsoft page about Excel and IEEE 754.
And please read David Goldberg's seminal What Every Computer Scientist Should Know About Floating-Point Arithmetic. It changed the way I understood floating point numbers.