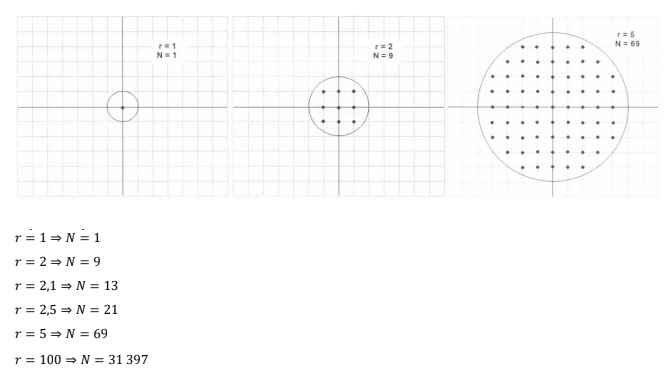
I am trying to write the program which will find points that have integer coords inside a circle. Program should read circle's radius from the user.

Sample correct answers are below picture

I need to write it using iteration and recursion. Iteration works correctly for radius=100:

 static int FindPointsByIteration(double minusRadius, double radius)
    {
        int result = 0;
        for (int x = (int)minusRadius; x <= (int)radius; x  = 1)
        {
            for (int y = (int)minusRadius; y <= (int)radius; y  = 1)
            {
                if (((x * x)   (y * y)) < (radius * radius)) result  ;

            }
        }
        return result;
    }

Max radius without stack overflow is 69 if I open EXE file. In VS it's 62. Is it possible to optimize it?

static int FindPointsByRecursion(double x, double y, double radius, int result)
    {
        //Console.WriteLine($"x: {x}, y: {y},radius: {radius}, result: {result}");
        if (((x * x)   (y * y)) < (radius * radius)) result  ;
        if (y >= -1 * (int)radius)
        {
            if (x <= (int)radius)
            {
                x  ;
                return FindPointsByRecursion(x, y, radius, result);
            }
            
            x = -1 * (int)radius;
            y--;
            return FindPointsByRecursion(x, y, radius, result);
        }
        return result;
    }

CodePudding user response：

Counting points in one quarter is a very good idea, but I think I found easier solution (of course with your help). Here's code that calls a method for the first time:

points=4* FindPointsByRecursion(radius, 1, (int)radius, points);
points = ((int)radius - 1) * 4   1;

And a counting method here:

static int FindPointsByRecursion(double radius, int x, int y, int points)
    {
        if (y < 1) return points;
        if ((x * x)   (y * y) < (int)(radius * radius))
        {
            points  ;
            return FindPointsByRecursion(radius, x   1, y, points);
        }
        else
        {
            x = 1;
            return FindPointsByRecursion(radius, x, y - 1, points);
        }
        return points;
    }

It needs only one method.

CodePudding user response：

I think you can simplified FindPointsByIteration by only accept one parameter: radius. The problem description states it is a circle (not an oval), it only features one radius. Moreover, radius is a scalar not a vector. It has the same quantity from any directions. Therefore, radius could also represent minusRadius. E.g.

static int FindPointsByIteration(double radius)
{
    int points = 0;

    for (int x = (int)-radius; x <= radius; x  )
    {
        for (int y = (int)-radius; y <= radius; y  )
        {
            if (((x * x)   (y * y)) < (radius * radius))
            {
                points  ;
            }
        }
    }
    return points;
}

Above function performs (2R)^2 iteration. FindPointsByIteration(2) takes 16 iterations. FindPointsByIteration(100) takes 40,000 iterations. For iteration, it is fine. For recursion, it may be too much. We need to think of another tactic.

As it is a circle, we can cut it into 4 quadrants. We only count the points in quadrant I and multiple it by 4, the result should be close to the solution. However, there is a catch. We should not multiple the origin and the point lie on the axis e.g.( [0,y] and [x,0]) since they share between quadrants.

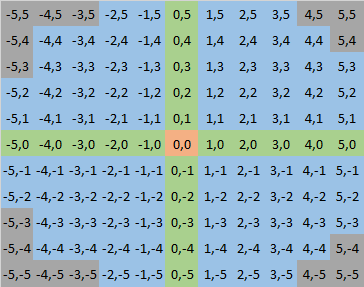
Consider a circle of radius 6:

There are 3 main category of its integer coordinate.

1. Origin (in red).

it is always [0,0]. Any circle should have one

2. Points on axis (in green).

It depends on the radius. Circle with radius > 1 would have. The number equals to the greatest integer less than the radius times 4.

3. Points inside quadrant (in blue)

Take quadrant I as example. We count the points by bottom-up, right-to-left approach. Start with [1,5] ([1,6] is known out-of-scope). If [1,5] is inside the scope, then the points for x:1 is 5. It is because any points smaller than 5 must be inside the scope (e.g. [1,4], [1,3] etc). Then we can move one row up at [2,5] and start the iteration again. Until you meet a point which is outside scope [4,5], then you move 1 column left [4,4] and start the iteration again. This way we can greatly reduce the number of recursion.

Example

static int FindPointsByRecursion(double radius)
{

    if (radius < 0) { return 0; }

    int points = 0;
    // origin
    if (radius > 0) { points  ; }
    // points on axis
    int longestEdge = IntegerSmallerThan(radius);
    points  = longestEdge * 4;
    // points contained in quadrant
    points  = FindPointsInQuadrant(1, longestEdge, radius) * 4;

    return points;
}

// return the greatest integer just smaller then n
static int IntegerSmallerThan(double n)
{
    int i = (int)n;
    return (n == i) ? --i : i;
}

static int FindPointsInQuadrant(int x, int y, double radius)
{
    // out of bound,  return 0
    if (x >= radius || y < 1) return 0;

    if ((x * x)   (y * y) < (radius * radius))
    {
        // if inside scope, move 1 row up
        return y   FindPointsInQuadrant(x   1, y, radius);
    }
    else
    {
        // if outside scope, move 1 column left
        return FindPointsInQuadrant(x, y - 1, radius);
    }
}

Main

Console.WriteLine("FindPointsByIteration");
Console.WriteLine(FindPointsByIteration(1));
Console.WriteLine(FindPointsByIteration(2));
Console.WriteLine(FindPointsByIteration(2.1));
Console.WriteLine(FindPointsByIteration(2.5));
Console.WriteLine(FindPointsByIteration(5));
Console.WriteLine(FindPointsByIteration(100));
Console.WriteLine("\nFindPointsByRecursion");
Console.WriteLine(FindPointsByRecursion(1));
Console.WriteLine(FindPointsByRecursion(2));
Console.WriteLine(FindPointsByRecursion(2.1));
Console.WriteLine(FindPointsByRecursion(2.5));
Console.WriteLine(FindPointsByRecursion(5));
Console.WriteLine(FindPointsByRecursion(100));

Output

FindPointsByIteration
1
9
13
21
69
31397

FindPointsByRecursion
1
9
13
21
69
31397