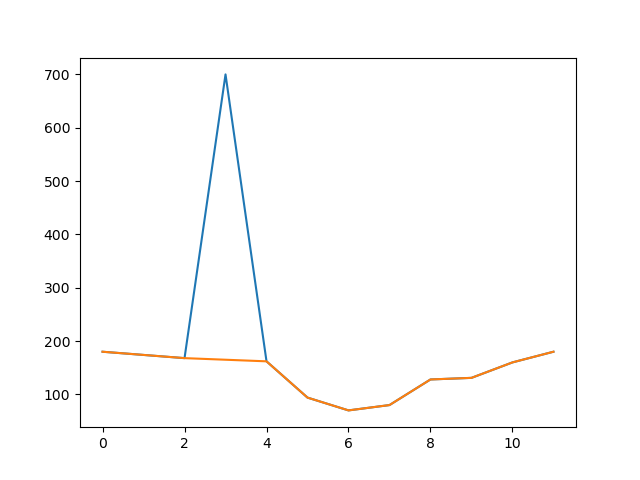
i'll explain for simple example then go into the deep if i have a list of number consist of

t_original = [180,174,168,166,162,94,70,80,128,131,160,180]

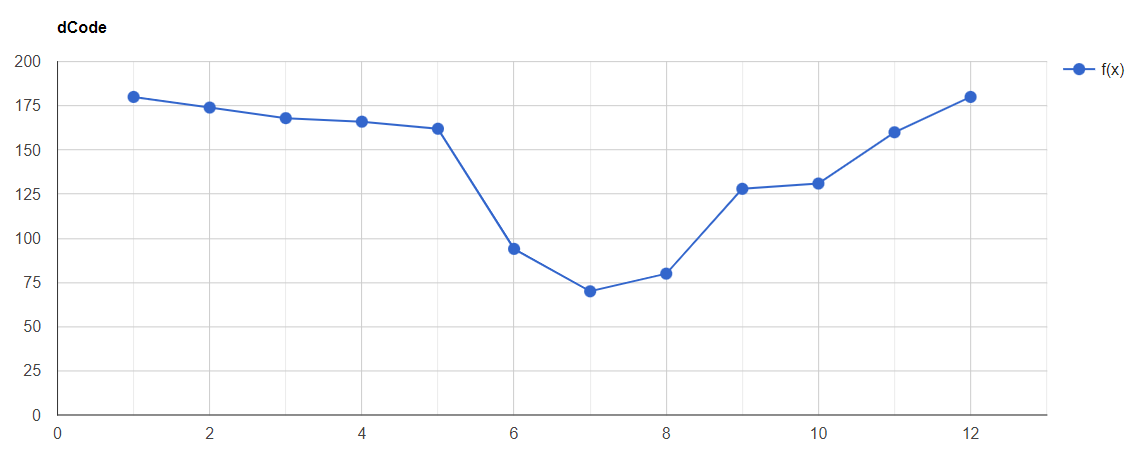
if we graph this so it goes down from 180 to 70 then it ups to 180 again

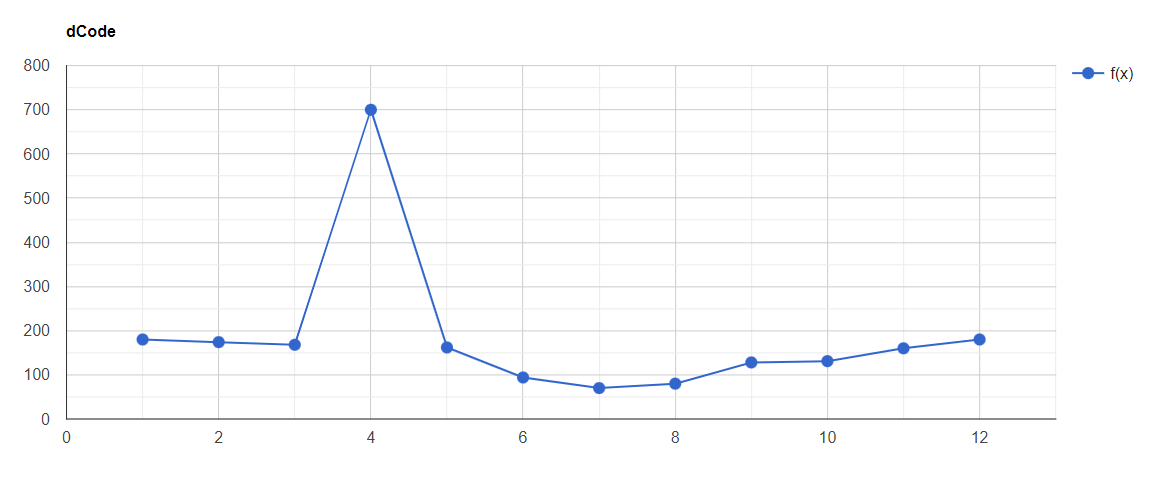
but if we suddenly change the fourth value (166) by 450 then the list will be

t = [180,174,168,700,162,94,70,80,128,131,160,180]

which dose not make sense in the graph

i wanna treat the fourth value (700) as a wrong value i want to replace it with a relative value even if not as the original value but relative to the previous two elements (168,174) i wanna do the same for the whole list if another wrong value appeared again

we can call that [Filling gaps between list of numbers]

so i'm tryig to do the same idea but for bigger example

the method i have tried

and i'll share my code with output , filtered means applied filling gap function

my code

def preprocFN(*U):
prePlst=[] # after preprocessing list
#preprocessing Fc =| 2*LF1 prev by 1 - LF2 prev by 2 |
c0 = -2     #(previous) by 2
c1 =-1      #(previous)
c2 =0       #(current)
c3 = 1      #(next)
preP = U[0] # original list
if c2 == 0:
    prePlst.append(preP[0])
    prePlst.append(preP[1])
    c1 =2
    c2 =2
    c0 =2
oldlen = len(preP)
while oldlen > c2:
    Equ = abs(2*preP[c1] - preP[c0]) #fn of preprocessing #removed abs()
    formatted_float = "{:.2f}".format(Equ) #with .2 number only
    equu = float(formatted_float)          #from string float to float
    prePlst.insert(c2,equu)      # insert the preprocessed value to the List
    c1 =1
    c2 =1
    c0 =1

return prePlst

with my input :

My Code :

def outLiersFN(*U):
outliers=[] # after preprocessing list
#preprocessing Fc =| 2*LF1 prev by 1 - LF2 prev by 2 |
c0 = -2     #(previous) by 2 #from original
c1 =-1      #(previous)      #from original
c2 =0       #(current)       #from original
c3 = 1      #(next)          #from original
preP = U[0] # original list
if c2 == 0:
    outliers.append(preP[0])
    c1 =1
    c2 =1
    c0 =1
    c3 =1
oldlen = len(preP)
M_RangeOfMotion = 90
while oldlen > c2 :
    if c3 == oldlen:
        outliers.insert(c2, preP[c2]) #preP[c2] >> last element in old list
        break
    if (preP[c2] > M_RangeOfMotion and preP[c2] < (preP[c1]   preP[c3])/2) or (preP[c2] < M_RangeOfMotion and preP[c2] > (preP[c1]   preP[c3])/2): #Check Paper 3.3.1
        Equ = (preP[c1]   preP[c3])/2 #fn of preprocessing # From third index # ==== inserting current frame
        formatted_float = "{:.2f}".format(Equ) #with .2 number only
        equu = float(formatted_float)          #from string float to float
        outliers.insert(c2,equu)      # insert the preprocessed value to the List
        c1 =1
        c2 =1
        c0 =1
        c3 =1
    else :
        Equ = preP[c2] # fn of preprocessing #put same element (do nothing)
        formatted_float = "{:.2f}".format(Equ)  # with .2 number only
        equu = float(formatted_float)  # from string float to float
        outliers.insert(c2, equu)  # insert the preprocessed value to the List
        c1  = 1
        c2  = 1
        c0  = 1
        c3  = 1
return outliers

CodePudding user response：

I suggest the following algorithm:

• data point t[i] is considered an outlier if it deviates from the average of t[i-2], t[i-1], t[i], t[i 1], t[i 2] by more than the standard deviation of these 5 elements.
• outliers are replaced by the average of the two elements around them.

import matplotlib.pyplot as plt
from statistics import mean, stdev

t = [180,174,168,700,162,94,70,80,128,131,160,180]

def smooth(t):
    new_t = []
    for i, x in enumerate(t):
        neighbourhood = t[max(i-2,0): i 3]
        m = mean(neighbourhood)
        s = stdev(neighbourhood, xbar=m)
        if abs(x - m) > s:
            x = ( t[i - 1   (i==0)*2]   t[i   1 - (i 1==len(t))*2] ) / 2
        new_t.append(x)
    return new_t

new_t = smooth(t)

plt.plot(t)
plt.plot(new_t)
plt.show()