DIfferent outcomes from autokriging and manual kriging-CodePudding

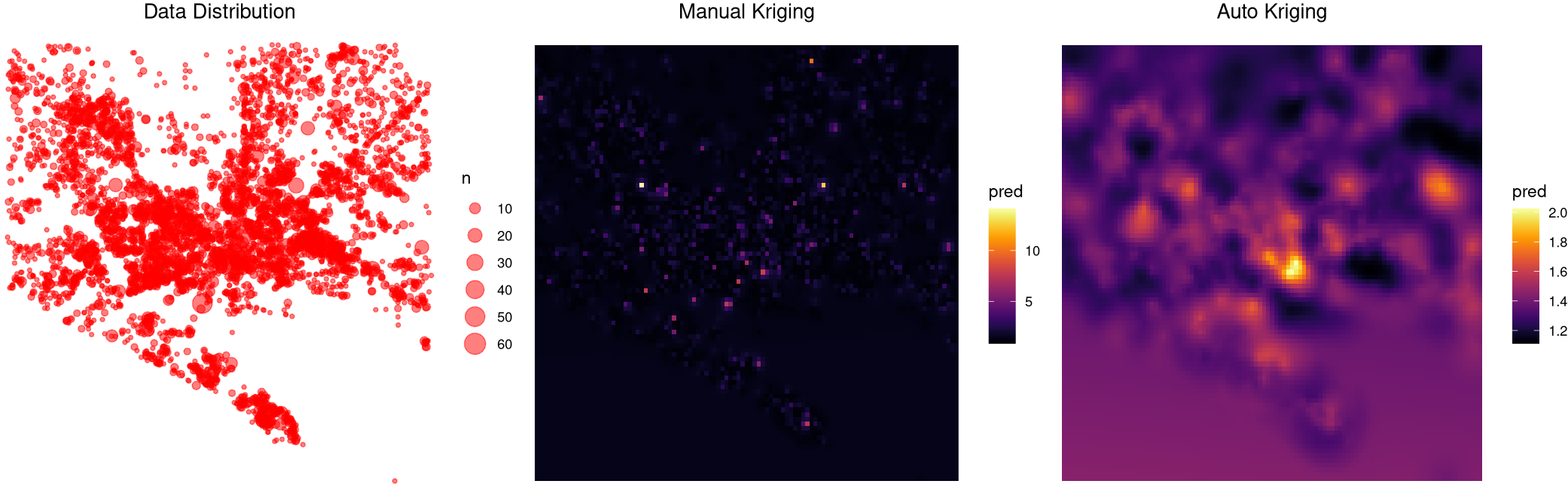
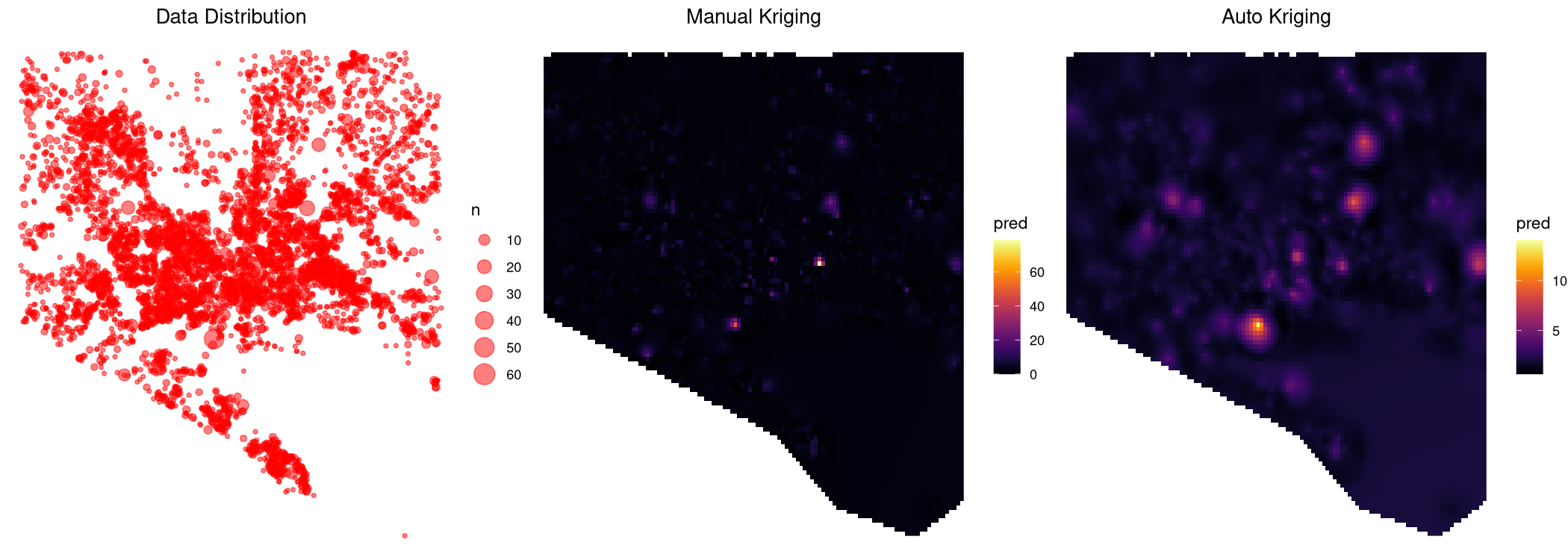
Can someone help me understand why I am getting such different results from auto- and manual kriging? I see the two algorithms are using different variogram models, but is that alone the reason for all the discrepancy? I am also uncomfortable with the fact that autokrige predicts significantly higher values at the locations where there is no data, e.g. bottom left and bottom right of the grid. Does it have to do with transforming the (log-transformed) kriged output back via exponentiation? Moreover, both methods predict much lower values than the data. It seems I am doing something wrong with either or both algorithm(s), any help is greatly appreciated.

EDIT:

CodePudding user response：

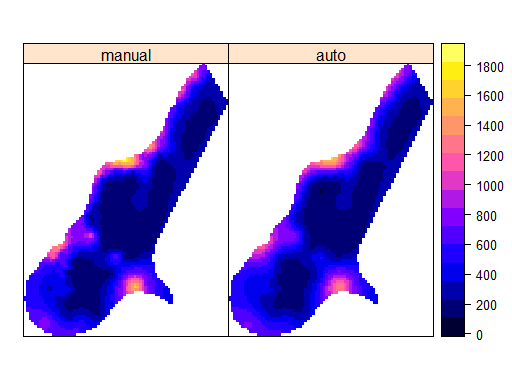
I think the problem is with your formula. It should be n ~ 1

Example data

library(gstat)
library(automap)
data(meuse)
coordinates(meuse) =~ x y
data(meuse.grid)
gridded(meuse.grid) =~ x y

Solution:

form <- zinc ~ 1

# manual
v <- variogram(form, meuse)
m <- fit.variogram(v, model=vgm(model=c("Sph", "Exp", "Mat", "Gau", "Ste")))
km <- krige(form, meuse, meuse.grid, model = m)

# auto
ka <- autoKrige(form, meuse, meuse.grid)

Have a look:

g <- cbind(km[,1], ka[[1]][,1])
names(g) <- c("manual", "auto")
spplot(g)

CodePudding user response：

Robert's answer above gave me the idea of trying the formula n ~ long lat (instead of log(n) ~ long lat I used before). Now the two methods seem to behave consistently with reasonable difference. I wonder if this is because of the skewness of my data, 70% of which has n = 1. Using log(n) in the earlier formula left only 30% non-zero values, leading to a sparse field with very little spatial correlation for krige to work with.

Note that meuse data in the example above does not have this problem: log(zinc) > 0 for all zinc values.