I am looking at a linear regression that cannot have points below its curve?-CodePudding

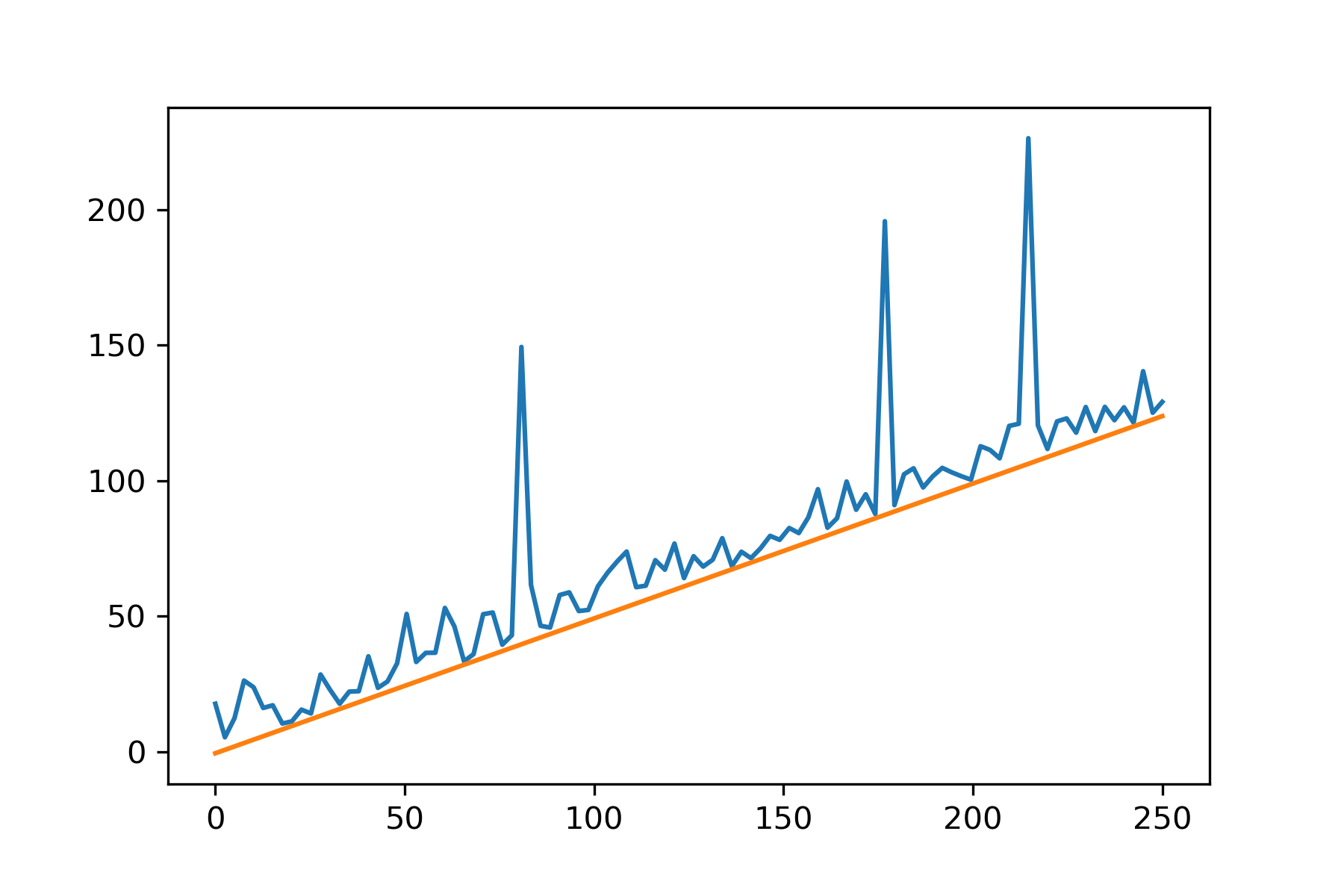
Basically, as shown in this image, i want to know if there is a linear regression model that allows to have all the points above its curve while still doing a linear regression. In this image, all the points with the lowest time are interesting as the excess time is only due to noise.

hence, is there a linear regression model that allows to have all the points above (or below) its curve while still doing a proper linear regression ?

#########################

here is an illustration of what i wish to obtain without using witchcratftry.

CodePudding user response：

Can I do a linear regression with the constraint that all points are above the curve ?

I don't think there is such a thing in scikit-learn but you can just minimize the square distance of your function from the points using scipy's minimize and have the constraint active while minimising.

First I generate an example

np.random.seed(0)
x = np.linspace(0,250,100)
y = 0.5*x np.abs(np.random.normal(0,10,x.shape))
y[np.random.randint(0,y.shape[0],3)]  = 100

I do your constrained least squares

def con(a):
    return np.min(y-(a[0]*x a[1]))

cons=({'type': 'ineq','fun': con})

def f(a):
    return np.linalg.norm(y-(a[0]*x a[1]))

x0 = [0.1,-1]

res = minimize(f, x0, constraints=cons)

And plot the result

a,b = res.x
plt.plot(x,y)
plt.plot(x,a*x b)