Should there be a correlation between an f1 score and the confusion matrix results in a gradient-boo-CodePudding

I'm building a decision tree model based on data from the "Give me some credit" Kaggle competition (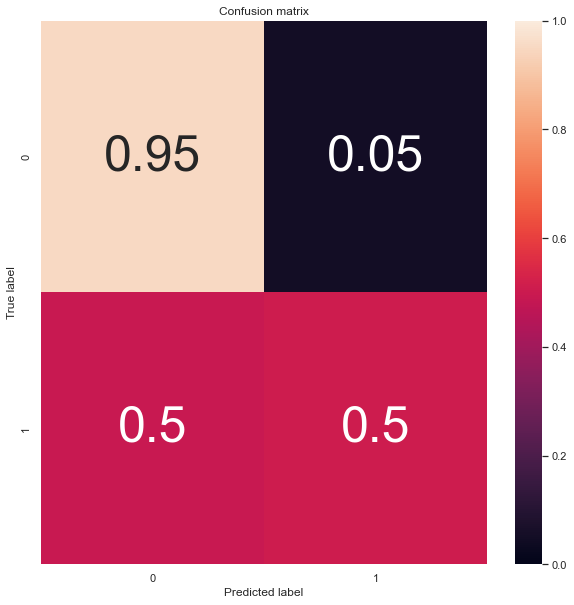

When attempting to tune the parameters in order to achieve better label prediction, I can improve the label prediction accuracy to 97% for both labels, however that decreases the f1 score to about 0.3. Here's the code I use for creating the confusion matrix (parameters included are the ones that have the f1 score of 0.3):

from xgboost import XGBClassifier
from numpy import nan
final_model = XGBClassifier(base_score=0.5, booster='gbtree', callbacks=None,
              colsample_bylevel=1, colsample_bynode=1, colsample_bytree=0.7,
              early_stopping_rounds=None, enable_categorical=False,
              eval_metric=None, gamma=0.2, gpu_id=0, grow_policy='depthwise',
              importance_type='gain', interaction_constraints='',
              learning_rate=1.5, max_bin=256, max_cat_to_onehot=4,
              max_delta_step=0, max_depth=5, max_leaves=0, min_child_weight=9,
              missing=nan, monotone_constraints='()', n_estimators=800,
              n_jobs=-1, num_parallel_tree=1, predictor='auto', random_state=0,
              reg_alpha=0, reg_lambda=1, scale_pos_weight=5)

final_model.fit(X,y)

pred_xgboost = final_model.predict(X)

cm = confusion_matrix(y, pred_xgboost)
cm_norm = cm/cm.sum(axis=1)[:, np.newaxis]
plt.figure()
fig, ax = plt.subplots(figsize=(10, 10))
plot_confusion_matrix(cm_norm, classes=rf.classes_)

And here's the confusion matrix for these parameters:

I don't understand why there is seemingly no correlation between these two metrics (f1 score and confusion matrix accuracy), perhaps a different scoring system would prove more useful?

CodePudding user response：

Would you kindly show the absolute values? Technically, cm_norm = cm/cm.sum(axis=1)[:, np.newaxis] would represent recall, not the accuracy. You can easily get a matrix with a good recall but poor precision for the positive class (e.g. [[9000, 300], [1, 30]]) - you can check your precision using the same code with axis=0. (F1 is the harmonic mean of your positive class recall and precision.)

If you wish to optimize for F1, you should also look for an optimal classification threshold on the sklearn.metrics.precision_recall_curve().

CodePudding user response：

It would help to understand it better if you generate the classification report too.

Also, a higher max_rate can change the value of Recall Specificity, which affects one of the class's f1_score in the classification report, but not the f1-score derived from f1_score(y_valid, predictions). Oversampling can also affect the Recall.

from sklearn.metrics import classification_report
ClassificationReport = classification_report(y_valid,predictions.round(),output_dict=True)

f1_score is the balance between precision and recall. The confusion matrix shows the precision values of both classes. With the classification report, I can see the relationship, like in the example below.

Classification Report
    precision   recall      f1-score    support
0   0.722292    0.922951    0.810385    23167.0
1   0.982273    0.923263    0.951854    107132.0


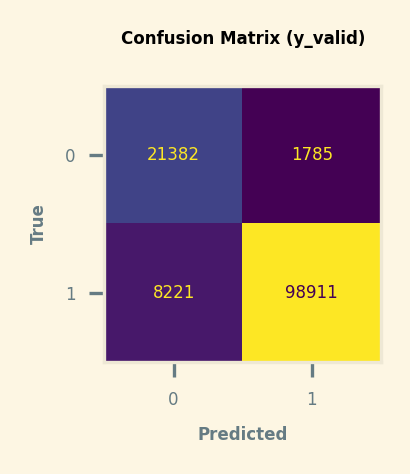
Confusion Matrix using Validation Data (y_valid)

True Negative  : CHGOFF (0) was predicted 21382 times correctly (72.23 %)
False Negative : CHGOFF (0) was predicted 8221 times incorrectly (27.77 %)
True Positive  : P I F (1) was predicted 98911 times correctly (98.23 %)
False Positive : P I F (1) was predicted 1785 times incorrectly (1.77 %)