Exponentially weighted moving variance in R-CodePudding

I am trying to write a R-function to calculate the exponentially weighted moving variance (EWMV). I only found R-packages for the simple moving variance (e.g. runSD in package TTR, roll_SD in package roll).

A formula to calculate EMWV can be found on wiki which refers to this paper.

I struggle in understanding the mathematics and transform them into a working function. Especially, I am note sure how to compute the EWMV "easily along with the moving average" as wiki suggests.

Here is a function to calculate the exponential moving average (EMA) (adapted, from this site):

EMA <- function (price,n){
  ema <- c()
  ema[1:(n-1)] <- NA
  ema[n]<- mean(price[1:n])
  alpha <- 2/(n 1)
  for (i in (n 1):length(price)){
    ema[i]<-alpha* price[i]   
      (1-alpha) * ema[i-1]
  }
  ema <- reclass(ema,price)
  return(ema)
}

I would be very grateful for some help and ideas on how to integrate the EMWV into this function. Thanks a lot!

Update: Thanks everyone for your ideas and codes. I reread the literature and based on your comments changed the code the following way:

EMVar <- function(x, n){
  alpha <- 2/(n 1)
  
  # exponential moving average
  ema <- c()
  ema[1:(n-1)] <- NA
  ema[n]<- mean(x[1:n])
  
    for (i in (n 1):length(x)){
    ema[i]<-alpha* x[i]   
      (1-alpha) * ema[i-1]
  }
  
  # exponential moving variance
  delta <- x - lag(ema)

  emvar <- c()
  emvar[1:(n-1)] <- NA
  emvar[n] <- ifelse(n==1,0,var(x[1:n]))
  
  for(i in (n 1):length(x)){
    emvar[i] <-  (1-alpha) * (emvar[i-1]   alpha * delta[i]^2)
  }
    return(emvar)  
}

Here are the main changes:

EMA[i] = EMA[i-1] alpha * delta is the same as alpha * x[i] (1-alpha) * EMA[i-1], which is the formule to calculate the exponential moving average. So there was no need in calculating it again. Also, one could use function EMA in package TTR. However, this function here calculates EMA as well and does not rely on other packages.
The description on wiki did not take different sliding windows into account. Instead, it started with x[1] and stated correctly that EMA[1] = x[1] and EMVar[1] = 0. However, this does not work with a slinding window of e.g. 20. For moving averages the simple mean is used in such situations (i.e. EMA[20] = mean(x[1:20])). Accordingly, I used the simple variance for the first value (i.e., EMVar[20] = var(x[1:20])).

CodePudding user response：

I'm not familiar with this theme, but can't you write the equations in a simple loop?

The equations are:

delta[i] <- price[i] - ema[i-1]
ema[i] <- ema[i-1]   alpha * delta[i]
emvar[i] <- (1-alpha) * (emvar[i-1]   alpha * delta[i]^2)

And we only need to create ema using the EMA function on your post, and assingn the emvar initial values for the loop. For the initial values, I assigned the first n values of the emvar as NA, and the nth 1 as (1-alpha)*(emvar[n] alpha*delta[n 1]^2) treating emvar[n] as 0 (which might be wrong, but as I said, i'm not familiar with this theme).

The delta values can be calculated outside the loop usign the function lag.

EMVar <- function(price, n){
  ema <- EMA(price, n)
  alpha <- 2/(n 1)
  delta <- price - lag(ema)
  
  emvar[1:n] <- rep(NA, n)
  emvar[n] <- (1-alpha) * alpha * delta[i]^2
  
  for(i in (n 1):length(price)){
    ema[i] = ema[i-1]   alpha * delta[i]
    emvar[i] = (1-alpha) * (emvar[i-1]   alpha * delta[i]^2)
  }
  
  emvar <- reclass(emvar, price)
  return(emvar)  
}

I also don't know where the reclass function is from, but I included it in the end, following the EMA function you presented.

CodePudding user response：

The following function will take a series of observations and return a two-column data frame containing the EMA and EMVar. It uses a default alpha value which can be changed as required, and an option to drop NA values:

EMA_EMV <- function(x, alpha = 2 / (length(x)   1), na.rm = FALSE) {
  
  if(na.rm) x <- x[!is.na(x)]
  EMA <- x[1]
  EMV <- 0
  
  if(length(x) > 1) {
    for(i in 2:length(x)) {
      delta <- x[i] - tail(EMA, 1)
      EMA[i] <- tail(EMA, 1)   alpha * delta
      EMV[i] <- (1 - alpha) * (tail(EMV, 1)   alpha * delta^2)
    }
  }
  return(data.frame(EMA, EMV))
}

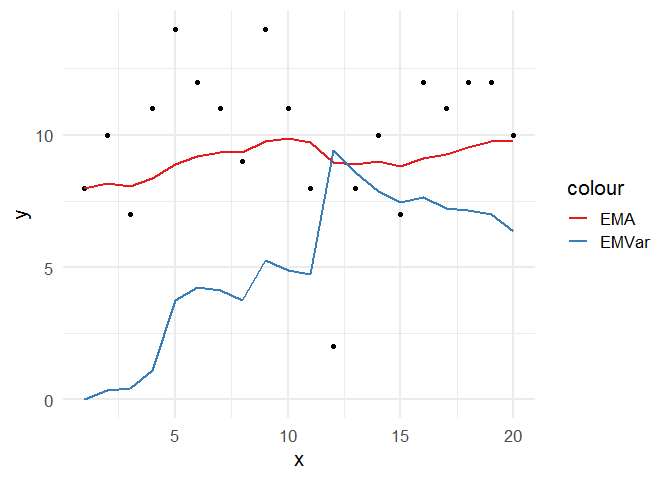
We can test it out on some random Poisson distributed data, where the mean and variance should both be around 10 on average:

set.seed(1)

df <- data.frame(x = 1:20, y = rpois(20, 10))

df2 <- EMA_EMV(df$y)

df2
#>         EMA       EMV
#> 1  8.000000 0.0000000
#> 2  8.190476 0.3446712
#> 3  8.077098 0.4339653
#> 4  8.355469 1.1287977
#> 5  8.893044 3.7666620
#> 6  9.188944 4.2397255
#> 7  9.361426 4.1185659
#> 8  9.327004 3.7375775
#> 9  9.772051 5.2632545
#> 10 9.888999 4.8919209
#> 11 9.709094 4.7334977
#> 12 8.974895 9.4036523
#> 13 8.882048 8.5899620
#> 14 8.988519 7.8795644
#> 15 8.799137 7.4698552
#> 16 9.103981 7.6412749
#> 17 9.284554 7.2232982
#> 18 9.543168 7.1707360
#> 19 9.777152 7.0079197
#> 20 9.798375 6.3447780

And we can plot the result like this:

library(ggplot2)

ggplot(cbind(df, df2), aes(x, y))  
  geom_point()  
  geom_line(aes(y = EMA, color = "EMA"), size = 1)  
  geom_line(aes(y = EMV, color = "EMVar"), size = 1)  
  scale_color_brewer(palette = "Set1")  
  theme_minimal(base_size = 16)

^{Created on 2022-06-18 by the reprex package (v2.0.1)}