Curve does not fit with the Histogram for Customize Function-CodePudding

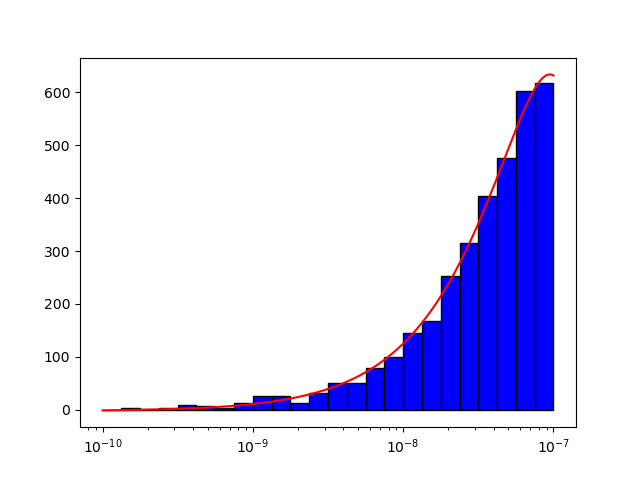
I am trying to fit a curve to a histogram, but the resulting curve is flat even though the histogram was not. How can I fit the curve correctly?

My current code:

import numpy as np

import matplotlib.pyplot as plt

from scipy.optimize import curve_fit

import pandas as pd

import scipy.optimize as optimization


x = np.random.normal(1e-10, 1e-7, size=10000)

def func(x, a, b, c):
    return a * (np.exp(-b*(x-c)**2))

bins=25

logbins = np.logspace(np.log10(1.0E-10),np.log10(1E-07),bins)


bin_heights, bin_borders, _ = plt.hist(x, bins=logbins, edgecolor='black', color='b')
bin_centers = bin_borders[:-1]   np.diff(bin_borders) / 2

x0    = np.array([0.0, 0.0, 0.0])

popt,cov = optimization.curve_fit(func, bin_centers, bin_heights,x0)
a,b,c=popt

popt, pcov = curve_fit(func, bin_centers, bin_heights, p0=[a,b,c])

x_interval_for_fit = np.linspace(bin_borders[0], bin_borders[-1], 1000)

plt.plot(x_interval_for_fit, func(x_interval_for_fit, *popt), label='Fit',color='r')


plt.xscale('log')

plt.show()

The result:

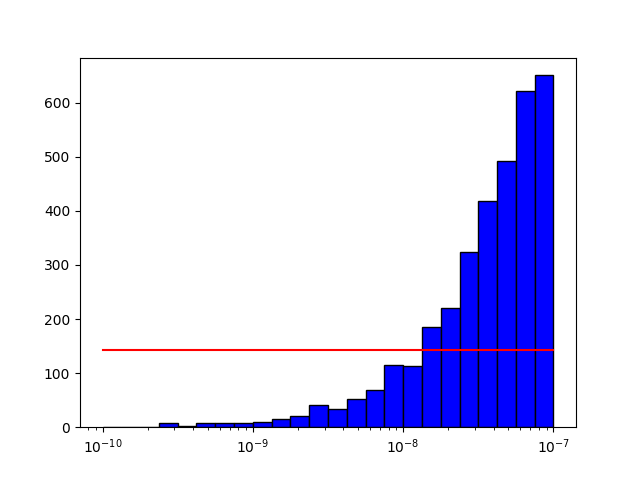
Screen shot showing my curve is flat but my histogram increases

CodePudding user response：

You are getting bad results because the function you are using to fit the histogram doesn't look like the shape of the histogram at all. By using a simple second order interpolation function, the results are a lot better (though you might say not ideal):

def func(x, a, b, c):
    return a * x**2   b * x   c  # Simple 2nd-order polynomial

Using it with your code (you can remove the two optimisation steps and do that only once), I got the following result:

One thing that may have been unintentional in your code is that, in spite of the fact that you created a normal distribution, on your histogram you decided to bin them in a surprising way: considering only what you have on one side of the distribution (since you start from 1e-10, and your distribution is centred in 1e-10) and you increase your bin size logarithmically to the right, you'll end up with more points on the larger bins. Also, you are ignoring more than half of your points (those the are smaller than 1e-10, check hist's