interpolate velocity for a curved mesh-CodePudding

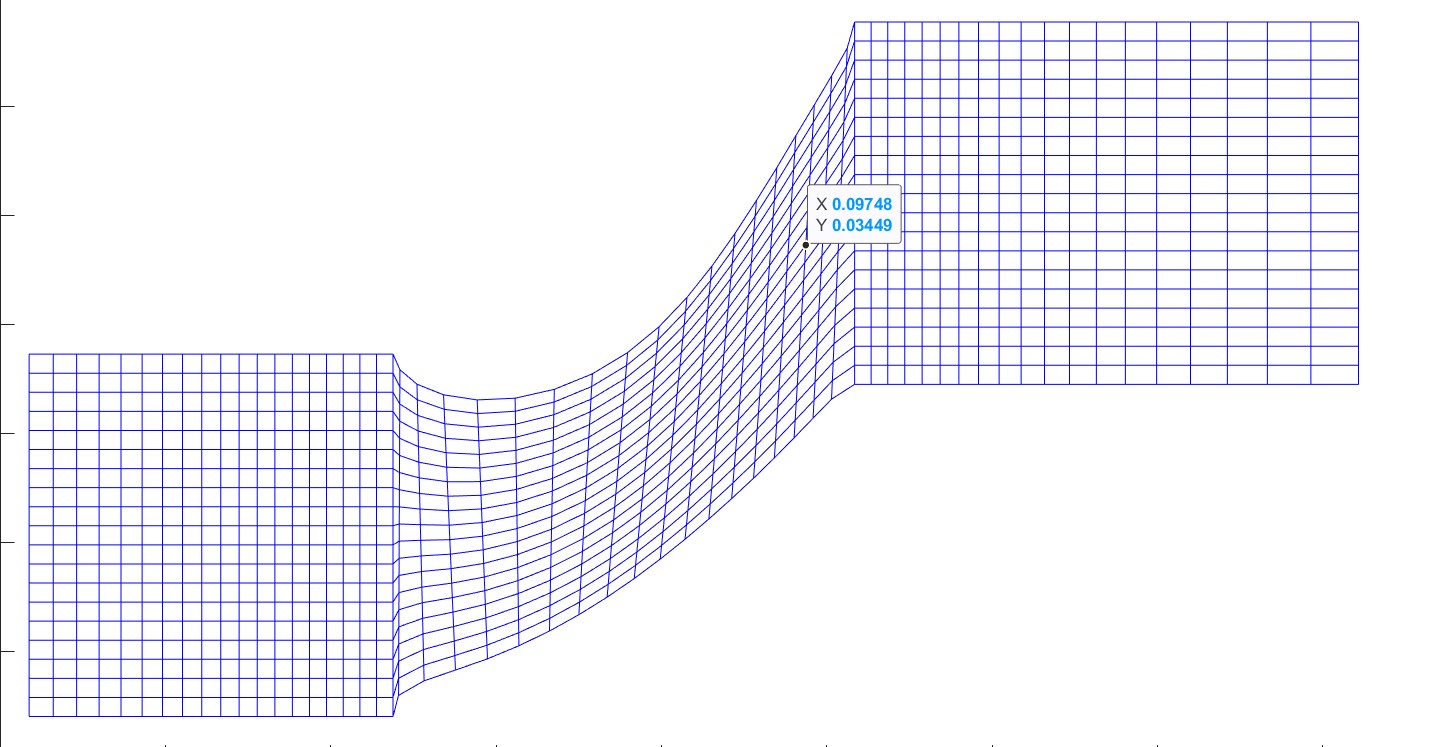
'x','y' and 'u' are 2D matrices for the x-coordinate, y-coordinate, and velocity of each node of the below mesh (figure). and I want to interpolate for (x_q,y_q) to find u_q for an arbitrary point(q).

My mesh is not rectangular and "interp2" error is: "Input grid is not a valid MESHGRID".

Any Ideal what can I do?

Thanks.

minimal reproducible example:

x=[0.0482114583977891,0.0482201588072998,0.0482288592168105;0.0513027685854806,0.0512573490659834,0.0512119412024664;0.0550957532853860,0.0550195888619688,0.0549437786953572;0.0589706773586289,0.0589051888951395,0.0588397004316502];
y=[-0.0481475644832381,-0.0450026617243515,-0.0418577589654650;-0.0454644879533678,-0.0426002662557475,-0.0397360636257961;-0.0434988768053532,-0.0408400599208391,-0.0381819554721181;-0.0414343539900984,-0.0389341351227583,-0.0364339162554183];
u=[1.52583130467469,14.3816671073665,58.5433654462735;108.677373003789,124.842139940676,145.468567077514;110.206733380171,111.157308056414,111.709609403516;135.414711548714,138.843419308648,147.988201447309];
xq=0.065;
yq=0.035;
uq = interp2(x,y,u,xq,yq,'cubic',0);

CodePudding user response：

Per Matlab documentation for the interp2 function, the requirements for cubic spline interpolation are:

Grid must have uniform spacing in each dimension, but the spacing does not have to be the same for all dimensions

Requires at least four points in each dimension

In the case of your code, neither of these conditions is met.

You would need to make sure that the x and y points are evenly spaced, ideally using meshgrid to generate the points and you would need to make the specified points, which are currently 3x4, at least 4x4.

Documentation for the function is found here: https://www.mathworks.com/help/matlab/ref/interp2.html

There is a response to a similar question here: https://www.mathworks.com/matlabcentral/answers/866695-input-grid-is-not-a-valid-meshgrid

CodePudding user response：

The interp2 function needs a regular grid (for instance something that was createed by meshgrid). In your case you have scattered data, in which case it you'd have to use griddata for interpolation:

uq = griddata(x,y,u,xq,yq, 'nearest');

(Note that in your MCVE your query point is way outside of the defined input points, so only 'nearest' will really work as a method.)