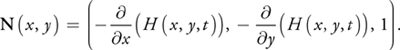Waterwave normals calculation slightly off-CodePudding

I implemented "The Sum of Sines Approximation" in this article:

The generation of the normals looks like this in the shader:

vec3 generateWaveSineSumNormal(sineParams _params[sineCount])
{
        vec2 pos = vec2(aPos.x, aPos.z);
        vec3 normal = vec3(0.0f, 1.0f, 0.0f);

        for(int i=0; i<sineCount; i  )
        {
            sinParams curParams = _params[i];
            normal.x  = sineExponent * curParams.direction.x * curParams.frequency * curParams.amplitude * 
                        pow((sin(dot(curParams.direction, pos) * curParams.frequency   curTime * curParams.speed) 1)/2, sineExponent-1)
                        * cos(dot(curParams.direction, pos) * curParams.frequency   curTime * curParams.speed);

            normal.z  = sineExponent * curParams.direction.y * curParams.frequency * curParams.amplitude * 
                        pow((sin(dot(curParams.direction, pos) * curParams.frequency   curTime * curParams.speed) 1)/2, sineExponent-1)
                        * cos(dot(curParams.direction, pos) * curParams.frequency   curTime * curParams.speed);
        }

        return vec3(-normal.x, normal.y, -normal.z);

}

When the x- and z-values are flipped like this, the normals are fine. I'm just wondering what I did wrong implementing it, since I just can't find it.

CodePudding user response：

Your normal.xz calculates the gradient of the heightmap correctly. The gradient points uphill, i.e. where the height values increase. The normal, when projected on the horizontal plane, would point backwards.

This can be derived mathematically through the use of cross-product of two tangents, which is what that article does in the "Normals and Tangents" section. In particular the relevant result is the formula for the normal in "Equation 6b", which includes the negative signs:

Equation 6b