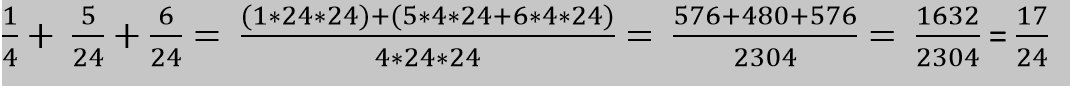i have a table like this:
| ID | num_A | num_B |
|---|---|---|
| 1 | 1 | 168 |
| 2 | 1 | 4 |
| 2 | 5 | 24 |
| 2 | 6 | 24 |
| 3 | 1 | 36 |
So, num_A and num_B represent a fraction. That means for ID=1, i have 1/168, ID=2 ---> (1/4) (5/24) (6/24) = 17/24, ID=3 --> 1/36....
I need to add 2 columns, one with the sum(num_A) and one with the denominator num_B, for those with the same ID. So the example should be:
| ID | num_A | num_B | sumA | denom_B |
|---|---|---|---|---|
| 1 | 1 | 168 | 1 | 168 |
| 2 | 1 | 4 | 17 | 24 |
| 2 | 5 | 24 | 17 | 24 |
| 2 | 6 | 24 | 17 | 24 |
| 3 | 1 | 36 | 1 | 36 |
My problem is that i dont know how to calculate the denominator for each different fraction in postgres.
CodePudding user response:
In general PostgreSQL provides the LCM function that returns the least common multiple (the smallest strictly positive number that is an integral multiple of both inputs), but it takes only two arguments and cannot be used to process rowset column values.
Thus, to get the LCM of rows with the same ID value, you can use a recursive CTE to process the rows one by one, using the LCM function with the LCM calculated in the previous step (in the first step equal to the value of num_B ) and the current value of num_B as arguments. This will produce the LCM value of all previous num_B and the current value for each row.
Finally, you can get the maximum (the last if to be exact, it would be the maximum anyway) calculated LCM value for rows grouped by ID and that will be the LCM for all num_B values with the same ID.
The rest is simple - divide, multiply and sum.
Query:
WITH t_rn AS (
SELECT *, ROW_NUMBER() OVER (PARTITION BY id ORDER BY num_b) AS rn FROM t
),
least_common_multiple AS (
WITH RECURSIVE least_multiples AS (
SELECT
id,
num_b,
num_b AS lm,
rn
FROM t_rn
WHERE rn = 1
UNION ALL
SELECT
t_rn.id,
t_rn.num_b,
LCM(t_rn.num_b, lm.lm),
t_rn.rn
FROM t_rn
JOIN least_multiples lm ON lm.id = t_rn.id AND t_rn.rn = lm.rn 1
)
SELECT
id,
MAX(lm) AS lcm
FROM least_multiples
GROUP BY id
)
SELECT
t.*,
SUM(t.num_a * lm.lcm / t.num_b) OVER (PARTITION BY t.id) AS suma,
lm.lcm AS denom_b
FROM t
JOIN least_common_multiple lm ON t.id = lm.id
Output
| id | num_a | num_b | suma | denom_b |
|---|---|---|---|---|
| 1 | 1 | 168 | 1 | 168 |
| 2 | 1 | 4 | 17 | 24 |
| 2 | 5 | 24 | 17 | 24 |
| 2 | 6 | 24 | 17 | 24 |
| 3 | 1 | 36 | 1 | 36 |
where the ROUND(EXP(SUM(LN(num_b)) over (partition by id))) will find the multiplication of the dividends for each id. (According to this post)