I am using matlab online to subtract a negative number very close to 0, from a positive number very close to 0, and am wondering why this doesn't result in significant roundoff error? Is matlab doing some kind of optimisation to use addition instead of subtraction?

CodePudding user response：

Numerical cancellation is a consequence of using floating point arithmetics and in that sense unrelated to the specific programming language being used. Matlab is thus also affected.

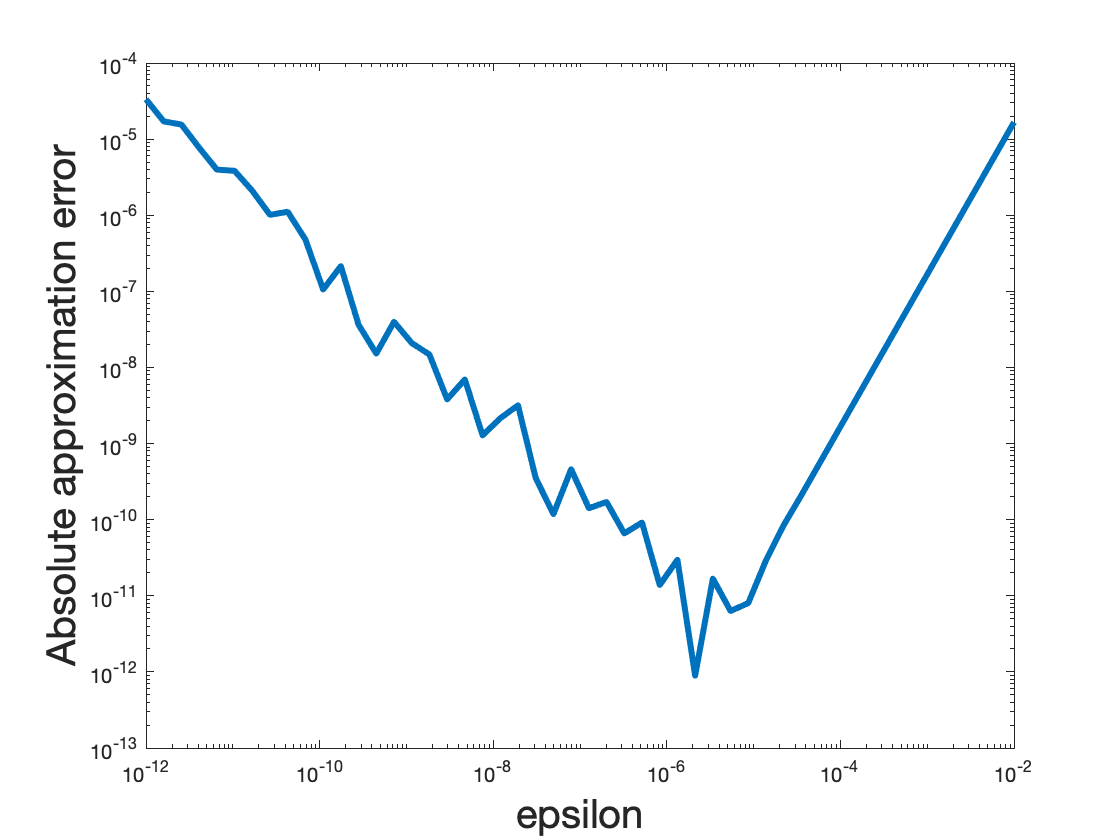
The code below shows the round-off error in a particular Matlab example. It calculates the finite difference approximation for the derivative of exp(x)-1 at the point x=0. The symmetric difference quotient requires exp( epsilon)-1 and exp(-epsilon)-1 thereby reproducing the subtraction of a slightly positive and slightly negative number. The absolute approximation error is clearly behaving erratic for small epsilon. This is the round-off error. The effect increases as epsilon is getting smaller (read: the values get closer together).

I can imagine two reasons as to why you did not observe the numerical round-off error.

1. The round-off error is quite small and might remain unobserved in practice.
2. There are specific situations in which rounding errors exactly cancel. For example, you might modify this code to compute the derivative of x^2 at x=0. However, the same rounding errors occur when calculating (-epsilon)^2 and ( epsilon)^2 and the numerical derivate works out just fine.

I hope this helps.

EpsilonList = logspace(-12,-2);

MyFunction = @(x) exp(x)-1;
TrueDerrivative = 1; % Derivative of exp(x)-1, exp(x), evaluated at x=0

% Initialize ErrorList
ErrorList = NaN(length(EpsilonList), 1);

%--- Compute ---%
for iter = 1:length(EpsilonList)
    
    % Increment
    epsilon = EpsilonList(iter);

    % Forward difference approximation
    FiniteDiffApprox = ( MyFunction(epsilon) - MyFunction(-epsilon) ) / (2*epsilon);

    % Approximation error
    DiffApproxError = FiniteDiffApprox - TrueDerrivative;

    % Store
    ErrorList(iter) = DiffApproxError;
end

%--- Create plot ---%
loglog(EpsilonList, abs(ErrorList), 'LineWidth', 3)
xlabel('epsilon', 'FontSize', 20)
ylabel('Absolute approximation error', 'FontSize', 20)

CodePudding user response：

Floating point numbers, in case of matlab, double by default, are represented by 3 parts: a sign bit (positive/negative), an exponent (11 bits, 1 for sign) and a fraction (52 bits), see the wikipedia page.

The value represented by doubles is

(-1)^{sign} * 1.{fraction} * 2^{exponent}

or

(-1)^{sign} * 0.{fraction} * 2^{exponent}

where {fraction} is the floating point part of the middle number. In the first case, two numbers with a {fraction} part of 0 (so a middle number of 1) will differ at least 2^{-52}. That is the value of eps in Matlab.

In the second case where the fraction also represents a very small number, the difference between two numbers can differ as little as 2^{-52} * 2^{-1022}.