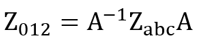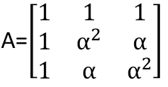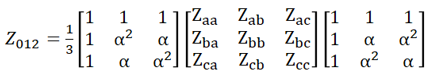I'm doing some symbolic matrix manipulations with complex value matrices. Some of my results are as below.

Zaa*(1   3i/36028797018963968)   Zab*(1   3i/36028797018963968)

Is there a way to tell Matlab to ignore those near zero imaginary results so the answer is reported simply as,

Zaa   Zab

UPDATE 1: To provide the full background on how I am getting these results. I am doing a calculation power electrical engineers call the similarity transformation. It is used in symmetrical component analysis of power system faults and involves a complex transformation matrix and complex impedance values (the later are my symbolic variables Zaa, Zab etc.).

Similarity transformation:

Where A is the 3x3 shown below and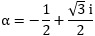

So, the full transformation calculation looks like this (the 1/3 scale factor comes from inverting A),

Here is my Matlab code (requires Symbolic Toolbox)

syms Zaa Zab Zac Zba Zbb Zbc Zca Zcb Zcc
Z = [Zaa Zab Zac; Zba Zbb Zbc; Zca Zcb Zcc]
a = -1/2 sqrt(3)/2*1i
A = [1 1 1; 1 a^2 a; 1 a a^2]
Z012 = inv(A)*Z*A

Final Update: After @holcher solved my problem I thought I'd post the finished code.

syms Zaa Zab Zac Zba Zbb Zbc Zca Zcb Zcc
Z = [Zaa Zab Zac; Zba Zbb Zbc; Zca Zcb Zcc]
a = -1/2 sqrt(sym(3))/2*1i
A = [1 1 1; 1 a^2 a; 1 a a^2]
Z012 = inv(A)*Z*A
vpa(Z012,2)

CodePudding user response：

First, why is this happening? It appears that you are mixing floating point values in with your symbolic math. Most numerical values do not have exact representations in floating point, resulting in small remainder values showing as in this case. The value 3/36028797018963968 is equal to (3/8)*eps. There are a few workarounds that may help you:

1. You can try representing parameters as symbolic variables and substituting in the floating point values later in your code via subs.
2. You can take care in how you convert floating point values to symbolic values. See this answer for more including a simple example of when this can occur. You might also take a look at the numeric conversion flag options for the sym function.
3. Consider using assumptions to restrict the domain of applicable symbolic variables to be real-valued if that is the case (Matlab symbolic variables are complex by default – this is why you will likely get a more complicated result if you call real or imag on your expression than you may expect). See assumptions, assume, and the options for syms.
4. Try calling simplify on a symbolic result prior to converting it to variable precision or floating point. The idea here is to possibly minimize mathematical operations that could contribute to numerical issues.

If none of those refactoring approaches work, you will need to write a function that evaluates your symbolic expression with a tolerance you specify for what you consider to be zero. This is non-trivial to implement in a general sense and is further complicated when working in the complex-valued domain.