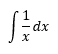R - which of these functions is giving the correct value of the integrals?-CodePudding

I am trying to compute this integral in R:

I found three functions which can be used for this and they are all giving me different results. Here is the code:

integrand <- function(x){
  r <- 1/x
  return(r)
}

First is the option from base R:

integrate(integrand,-Inf, Inf)

Giving the result:

0 with absolute error < 0

The second is from the pracma package:

quadinf(integrand, -Inf, Inf)

Giving this output:

$Q
[1] -106.227

$relerr
[1] 108.0135

$niter
[1] 7

And the last one is from the cubature package:

cubintegrate(integrand, -Inf, Inf)

Which gives the following result:

$integral
[1] Inf

$error
[1] NaN

$neval
[1] 15

$returnCode
[1] 0

So then, which one of these is correct and which should I trust? Is it 0, infinity, or -106.227? Why are they all different in the first place?

CodePudding user response：

1/x isn't integrable in [-Inf,Inf] range, because not integrable in 0.

On an integrable range, results are similar:

integrate(\(x) 1/x,1,2)
#0.6931472 with absolute error < 7.7e-15

pracma::quadinf( \(x) 1/x,1,2)
#$Q
#[1] 0.6931472

#$relerr
#[1] 7.993606e-15

#$niter
#[1] 4

Note that integral of 1/x in ]0,Inf] range is log(x):

log(2)-log(1)
#[1] 0.6931472