I'm trying to estimate the parameters (v, n, k) defined in fit_func. I tried the default least squares fit but I couldn't find the parameters successfully.

def fit_func(x, v, n, k):
    return v * x ** n / (k ** n   x ** n)

x = [2.5,         2.71317829,  4.08,        4.18604651,  5.19379845,  6.92,
 7.98449612,  8.94,        9.92248062,  9.94,       12.36,       13.48837209]
y = [0.16054661, 0.14643943, 0.11639118, 0.11796543, 0.15609638, 0.29527088,
 0.40774818, 0.51331307, 0.6163489,  0.61807529, 0.78372639, 0.78643515]
popt, pcov = curve_fit(fit_func, x, y)
print(popt)
plt.plot(x, y, '*')
plt.plot(x, fit_func(x, *popt), 'r')
plt.show()

I get the following error:

    raise RuntimeError("Optimal parameters not found: "   errmsg)
RuntimeError: Optimal parameters not found: Number of calls to function has reached maxfev = 800.

I'm not sure if I have selected the right method. Suggestions on alternate methods that I could use to estimate the parameters will be really helpful.

CodePudding user response：

The function y(x) = v * x ** n / (k ** n x ** n) = v / (k ** n * x ** (-n) 1) is strictly increasing or decreasing not both. This is not the shape convenient for the data : See the figure below. This can be a cause of bad fitting.

Another possible cause of failure might be the initial values of the parameters v , k , n which have to be set in order to start the iterative computation for non-linear regression.

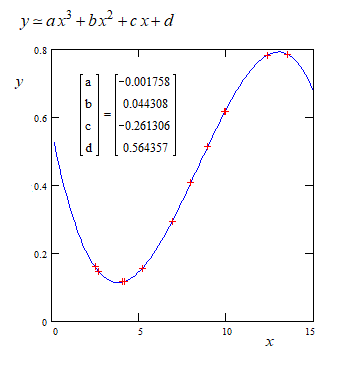
Just looking at the graph of the points distribution one can see that a cubic function would be more convenient. This is much simpler because the regression is linear and doesn't require initial guess of the parameters. The fitting is very good.