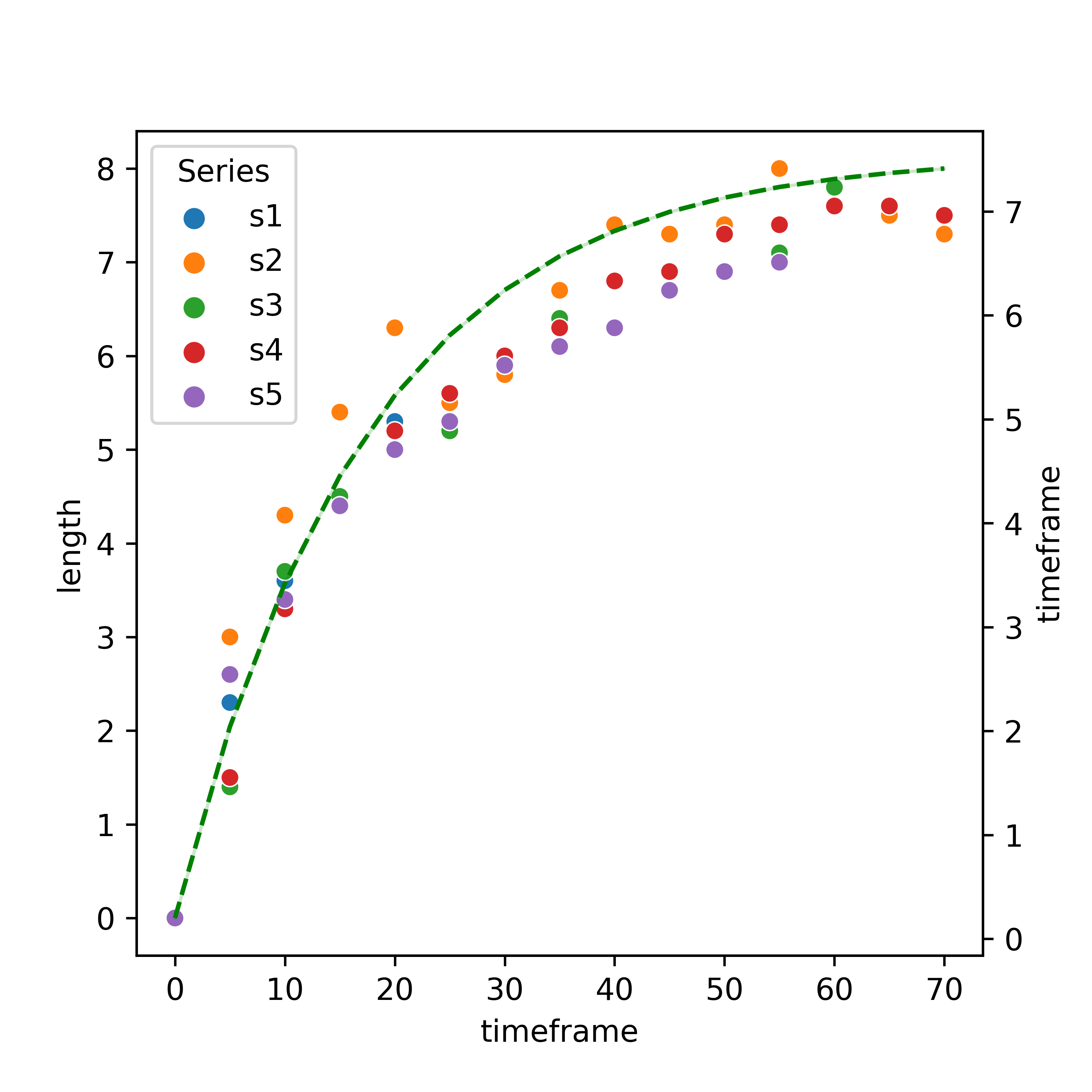
I am trying to fit an exponential curve into my data. However, I am having some trouble defining the x_value model properly in order to have a representative curve-fit to the data. I would think that the approach I used in preparing the DataFrame dataTable, is not optimal in the subsequent steps. I tried using arange() function to define x_line, but I wasn't successful. I would appreciate some help. See the table, the sample code I used, and the output.
Code
import os
import pandas as pd
import seaborn as sns
import numpy as np
import matplotlib.pyplot as plt
from numpy import exp
from scipy.optimize import curve_fit
# file path
folder = '...'
fileTable = os.listdir(folder)
for i in fileTable:
if i.endswith('.csv'):
df = pd.read_csv(i, index_col=None)
# creat a new table
series_df = df.loc[:, df.columns.str.startswith('s')]
time_df = df.loc[:, df.columns.str.startswith('timeframe')]
df_new = [series_df, time_df]
newTable = pd.concat(df_new, axis =1)
dataTable = newTable.melt('timeframe', var_name='Series', value_name='length').dropna()
x, y = dataTable['timeframe'], dataTable['length']
# plot the data
plt.figure(figsize=(5,5))
ax1 = sns.scatterplot(data=dataTable, x=x, y=y, hue = 'Series')
# define a function for an exponential curve
def exponential(x, a, b, c):
return a*(1-exp(-x / b)) c
popt, _ = curve_fit(exponential, x, y)
a, b, c = popt
x_line = x
y_line = exponential(x, a, b, c)
# plot the fit on top of the raw data
axs = ax1.twinx()
ax2 =sns.lineplot(data=dataTable, x=x, y=y_line, color='green', alpha=1, ax=axs)
ax2.lines[0].set_linestyle('--')
CodePudding user response:
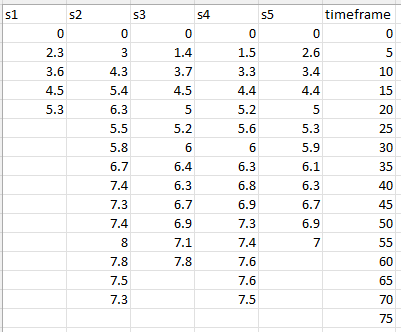
below data table in numerical format. Thanks.
| s1 | s2 | s3 | s4 | s5 | timeframe |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 |
| 2.3 | 3 | 1.4 | 1.5 | 2.6 | 5 |
| 3.6 | 4.3 | 3.7 | 3.3 | 3.4 | 10 |
| 4.5 | 5.4 | 4.5 | 4.4 | 4.4 | 15 |
| 5.3 | 6.3 | 5 | 5.2 | 5 | 20 |
| 5.5 | 5.2 | 5.6 | 5.3 | 25 | |
| 5.8 | 6 | 6 | 5.9 | 30 | |
| 6.7 | 6.4 | 6.3 | 6.1 | 35 | |
| 7.4 | 6.3 | 6.8 | 6.3 | 40 | |
| 7.3 | 6.7 | 6.9 | 6.7 | 45 | |
| 7.4 | 6.9 | 7.3 | 6. | 50 | |
| 8 | 7.1 | 7.4 | 7 | 55 | |
| 7.8 | 7.8 | 7.6 | 60 | ||
| 7.5 | 7.6 | 65 | |||
| 7.3 | 7.5 | 70 | |||
| 75 |
CodePudding user response:
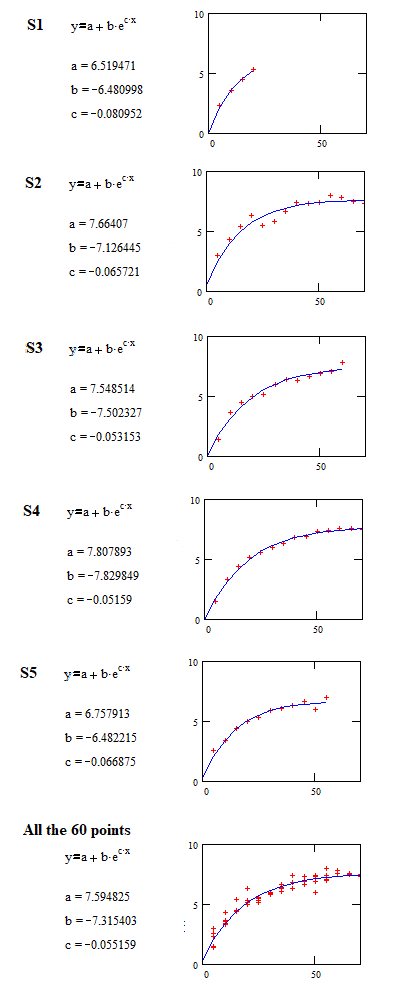
Below this is more a comment than a definitive answer to the question.
I used another software than yours to fit the function y = a b * exp( c * x) to your data.
See below the results with the data files S1 , S2 , S3 , S4 and S5 independently.
Then the five files where merged leading to a data of 60 points. The result of fitting to the exponential function is given at the bottom of next page.
I see no inconsistency.
So I suggest to first merge the five partial files into a unique file. Then import this big data file into a new session of your software for the nonlinear regression in order to avoid confusion with the previous calculus.
Nonlinear regression involves an iterative process. To start the process some "guessed" values of the unknown parameters are required. Possibly your software initiate the process with values not good enough. The values found above can be used as good initial values for a better relability.
NOTE :
For my above calculus I used the next very simple method :
Ref. : https://fr.scribd.com/doc/14674814/Regressions-et-equations-integrales .
One could improve a bit the accuracy with a post-treatment by nonlinear regression initiated with the above values of the parameters.