w1 <- 1000

w2 <- 600

a <- c(w1,w2)
fun1 <- function(a){
  return(exp(1)^1.5*a[1]^0.2*a[2]^(1-0.2))
}

#constraint - a[1] a[2]=10000

Answer1 <- constrOptim(c(w1,w2), fun1, NULL,
                       ui = c(1,1), ci = c(10000),
                       control = list(fnscale = -1))

Trying to optimize the function However, getting an error

"Error in constrOptim(c(1, 1), fun1, NULL, ui = c(1, 1), ci = c(10000),  : 
  initial value is not in the interior of the feasible region"

What could be the issue?

CodePudding user response：

You can consider the following approach :

library(DEoptim)

fun1 <- function(a1)
{
  a2 <- 10000 - a1
  val <- exp(1) ^ 1.5 * a1 ^ 0.2 * a2 ^ 0.8
  
  if(is.na(val) | is.nan(val))
  {
    return(10 ^ 30)

  }else
  {
    return(-val)
  }  
}

obj_DEoptim <- DEoptim(fn = fun1, lower = 0, upper = 10000)
obj_DEoptim$optim$bestmem

CodePudding user response：

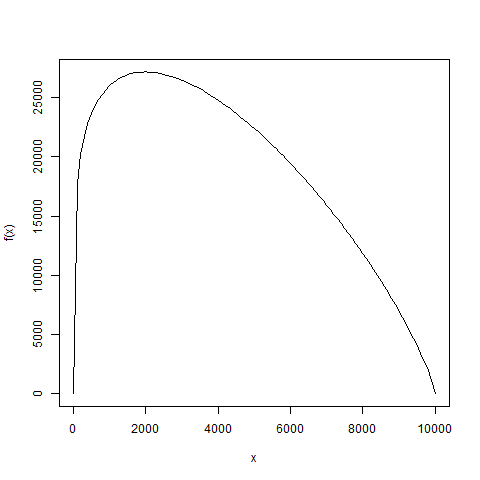
Note that you have an "equality" constraint consisting of only two variables, which actually can be denoted by x and 10000-x respectively. In this case, optim is sufficient for your purpose, e.g.,

f <- function(x) {
  return(exp(1.5) * x^0.2 * (10000 - x)^(1 - 0.2))
}

optim(1000,
  f,
  method = "Brent", 
  lower = 0, 
  upper = 10000, 
  control = list(fnscale = -1)
)

and you will obtain

$par
[1] 2000

$value
[1] 27171.88

$counts
function gradient
      NA       NA

$convergence
[1] 0

$message
NULL

By the way, you can visualize the cost function f using curve(f, 0, 10000), which shows