A shortest path with fuel constraints using Floyd-Warshall-CodePudding

I tried to write pseudo-code based on this solution. But I couldn't understand this part "Once we have run Bellman-Ford, we can look back at the results from Floyd-Warshall to determine whice partial paths corresponded to the path found in G'". Can anyone help me to understand this using pseudo-code?

CodePudding user response：

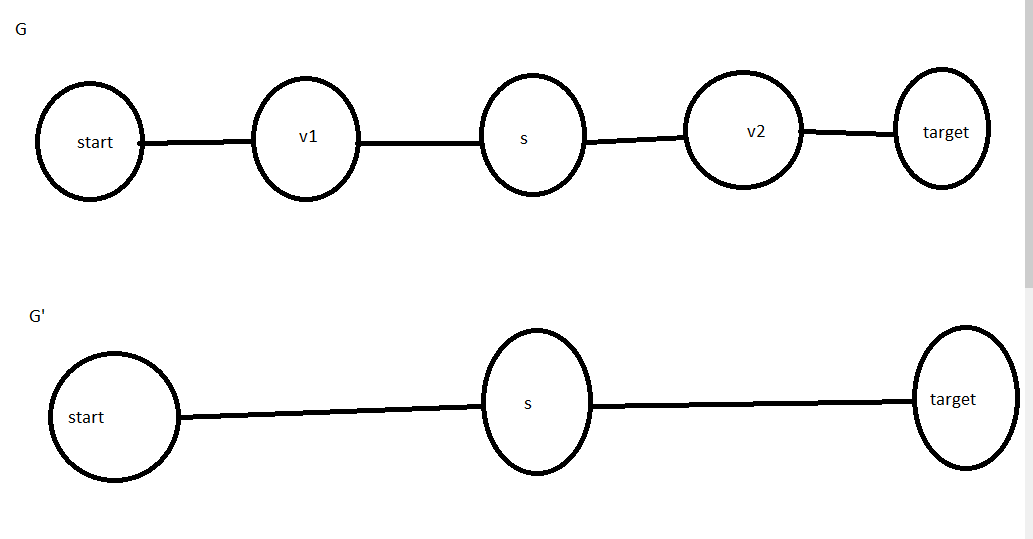
Let's look at a very simple example, with one gas station.

Find the shortest path in G' is start - s - target

To find the corresponding path in G, look at each hop in the G' path and find the shortest feasible path in G between the nodes in G1 hop'

start - s becomes start - v1 - s

s - target becomes s - v2 - target

Adding the partial paths together we get the answer

start - v1 - s - v2 - target

So the pseudo code is

Construct G'
Find P' the shortest path in G'
LOOP over hops in P'
    Find Pg shortest path between hop source and hop destination in G
    Add Pg to Ps ( eliminating common vertex )
Output Ps