I'm trying to solve this problem from my textbook:

When a frisbee is thrown into a bucket, it gets stuck where the inner diameter of the bucket is smaller than the outer diameter of the frisbee. Analyse where in the bucket the frisbees gets stuck given the dimensions of the bucket and the radius of the frisbees. The bucket is always empty when a new frisbee is thrown, so they don't pile up in the bucket.

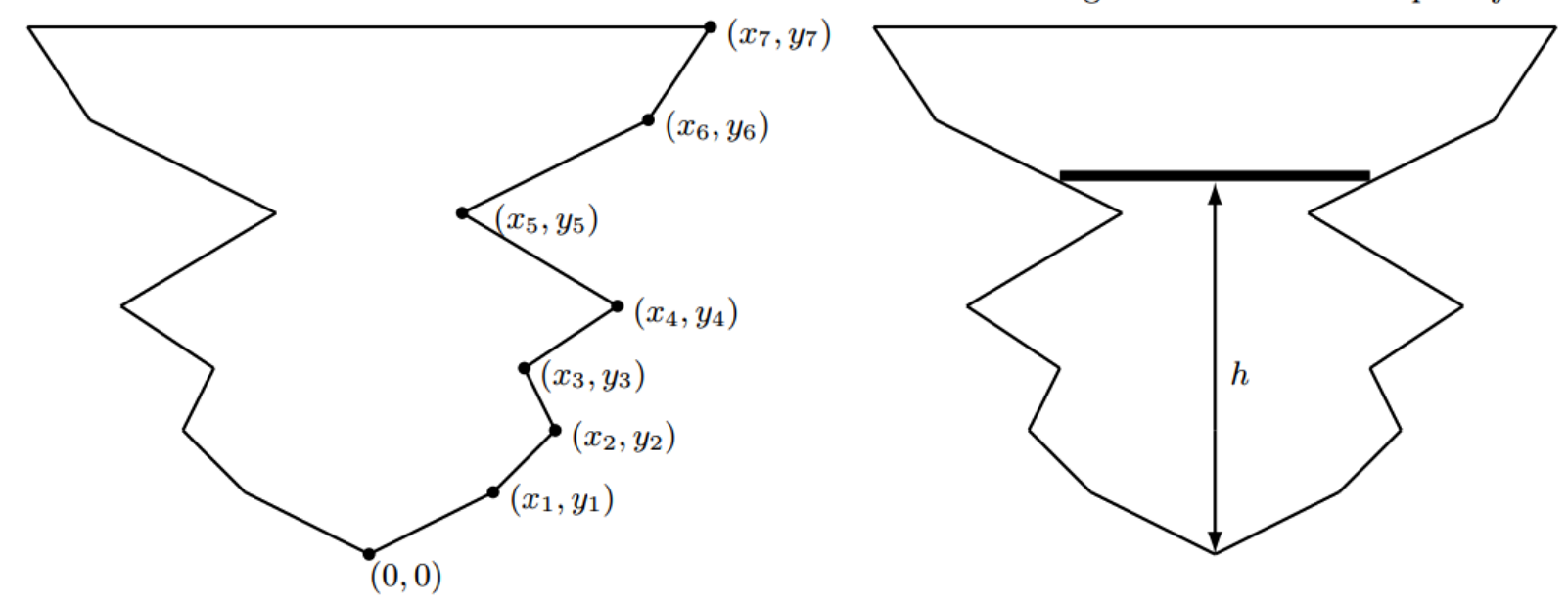
The bucket is symmetric along the y-axis. The picture shows what the cross section of the bucket can look like. The walls of the bucket are line segments that always connect at origo.

Input: (x_1,y_1),...,(x_m,y_m),r_1,...,r_n, all numbers are positive, m≤n and y_1 < y_2 < ...<y_m. (x_i,y_i) are the coordinates of the wall of the bucket, from the bottom to the top. r_i is the radius of the frisbee i.

Output: h_1,...h_n, where h_1 ≤ h_2 ≤...≤ h_n These are the different heights (y-coordinates) where the frisbees get stuck. The algorithm should be as efficient as possible.

My idea:

I sort the frisbees in a descending order. Then I take the first frisbee (largest) and iterate through all the points in the bucket until I find points with smaller x-values than the radius of the frisbee. The I calculate the point of intersection to get the y-coordinate. Then I push the y-coordinate to a stack to get the ordering right. When I take the second frisbee I know that the radius will be smaller or equal to the previous frisbee, so I know that the intersection will be at the same height or lower than the previous frisbee and I don't need to iterate through the same points of the bucket. Thus, I have reduced all redundancy. To get the right output I pop from the stack.

Is this the most optimal way to solve the problem in terms of time complexity in regards to the size of n?

My hypothesis is that the time complexity will be O(nlogn n m) = O(nlogn) since m is lesser or equal to n, since the sorting will take O(nlogn) time and the rest of the algorithm will take O(n m) since we iterate through n and m once each.

However it does seem kind of off-putting that the sorting will be the dominant factor of the time-complexity and not the algorithm itself. That's why I'm a bit concerned about this solution and it it's really the most optimal algorithm.

Is it possible to get the same/faster time complexity without ordering the frisbees?

Thanks in advance!

CodePudding user response：

A lot of great algorithms have complexities that are dominated by an initial sort, so that really shouldn't set off any alarm bells for you.

Since the problem statement indicates that there are more frisbees than bucket segments, though, the complexity of O(n log n m) that you achieve isn't quite optimal.

Note that a frisbee can only get stuck on the segment above a point that has a smaller x than all the points above it. Start by making a list of these points in y order, which you can do easily in O(m) time.

Because every point in the list has a smaller x than all the points after it, the list is monotonically increasing in x. For each frisbee, therefore, you can do a binary search in the list to find the last point with x < r. This takes O(log m) per frisbee for a total time of O(n log m m), which is strictly smaller than O(n log n m).

CodePudding user response：

The worst case is when every frisbee lands on a different segment, and that's possible if m = n and if, for all j and i such that 0 < j < i, x_j < x_i. From there, the problem amounts to sorting the list of frisbees. So the complexity of the solution is indeed dominated by the sorting.

However, the complexity of sorting isn't necessarily O(n log n). If the maximum size of a frisbee has a limit l, and if l < n, then using radix sort will lower the complexity to O(n log l) (where log l is the number of digits of l or "key length").