I want to solve the following optimization problem using Gekko in python 3.7 window version.

Original Problem

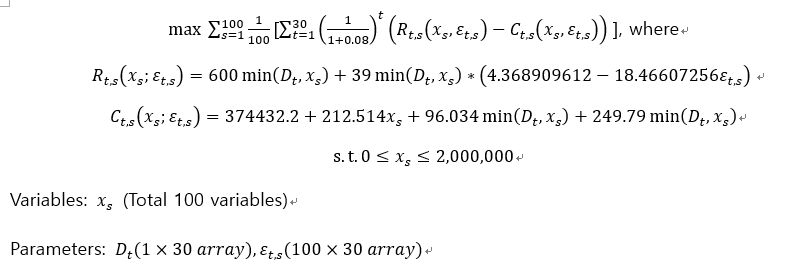
Here, x_s are continuous variables, D and Epsilon are deterministic and they are also parameters.

However, since minimization function exists in the objective function, I remove it using binary variables(z1, z2) and then the problem becomes MINLP as follows.

Modified problem

With Gekko,

(1) Can both original problem & modified problem be solved?

(2) How can I code summation in the objective function and also D & epsilon which are parameters in Gekko?

Thanks in advance.

CodePudding user response：

Both problems should be feasible with Gekko but the original appears easier to solve. Here are a few suggestions for the original problem:

• Use m.Maximize() for the objective
• Use sum() for the inner summation and m.sum() for outer summation for the objective function. I switch to m.sum() when the summation would create an expression that is over 15,000 characters. Using sum() creates one long expression and m.sum() breaks the summation into pieces but takes longer to compile.
• Use m.min3() for the min(Dt,xs) terms or slack variables s with x[i] s[i]=D[i]. It appears that Dt (size 30) is an upper bound, but it has different dimensions that xs (size 100). Slack variables are much more efficient than using binary variables.

D = np.array(100)
x = m.Array(m.Var,100,lb=0,ub=2000000)

The modified problem has 6000 binary variables and 100 continuous variables. There are 2^6000 potential combinations of those variables so it may take a while to solve, even with the efficient branch and bound method of APOPT. Here are a few suggestions for the modified problem:

• Use matrix multiplications when possible. Below is an example of matrix operations with Gekko.

from gekko import GEKKO
import numpy as np
m = GEKKO(remote=False)
ni = 3; nj = 2; nk = 4
# solve AX=B
A = m.Array(m.Var,(ni,nj),lb=0)
X = m.Array(m.Var,(nj,nk),lb=0)
AX = np.dot(A,X)
B = m.Array(m.Var,(ni,nk),lb=0)
# equality constraints
m.Equations([AX[i,j]==B[i,j] for i in range(ni) \
                             for j in range(nk)])
m.Equation(5==m.sum([m.sum([A[i][j] for i in range(ni)]) \
                                    for j in range(nj)]))
m.Equation(2==m.sum([m.sum([X[i][j] for i in range(nj)]) \
                                    for j in range(nk)]))
# objective function
m.Minimize(m.sum([m.sum([B[i][j] for i in range(ni)]) \
                                 for j in range(nk)]))
m.solve()
print(A)
print(X)
print(B)

• Declare z1 and z2 variables as integer type with integer=True. Here is more information on using the integer type.
• Solve locally with m=GEKKO(remote=False). The processing time will be large and the public server resets connections and deletes jobs every day. Switch to local mode to avoid a potential disruption.