First Derivative of Scatter Plot R-CodePudding

Hello I am working with sigmoidal data and am attempting to plot two scatter plots on top of each other: the raw data & the first derivative of the raw data. My issue doesn't lie in plotting the data, but more-so finding a function that will create an accurate representation of the first derivative.

What have I tried: Creating a function that calculates the slope of the current & next point: (y2-y1)/(x2-x1) & assigning the value to the current temperature.

dput() of Data Frame: structure(list(Temperature = c(4.98, 5.49, 6.01, 6.5, 7.02, 7.52, 8.03, 8.52, 9.03, 9.54, 10.04, 10.54, 11.05, 11.55, 12.05, 12.55, 13.05, 13.56, 14.06, 14.57, 15.07, 15.57, 16.07, 16.59, 17.08, 17.59, 18.08, 18.59, 19.09, 19.6, 20.1, 20.64, 21.12, 21.63, 22.13, 22.62, 23.13, 23.63, 24.13, 24.63, 25.11, 25.62, 26.11, 26.68, 27.19, 27.7, 28.2, 28.71, 29.21, 29.71, 30.21, 30.7, 31.21, 31.69, 32.19, 32.69, 33.19, 33.7, 34.19, 34.68, 35.19, 35.68, 36.19, 36.69, 37.19, 37.7, 38.19, 38.7, 39.2, 39.7, 40.21, 40.7, 41.22, 41.71, 42.21, 42.71, 43.21, 43.72, 44.22, 44.72, 45.22, 45.73, 46.23, 46.73, 47.23, 47.97, 48.71, 49.23, 49.74, 50.23, 50.73, 51.23, 51.73, 52.24, 52.75, 53.24, 53.75, 54.24, 54.75, 55.26, 55.75, 56.25, 56.75, 57.24, 57.75, 58.27, 58.77, 59.26, 59.77, 60.26, 60.78, 61.27, 61.79, 62.27, 62.77, 63.29, 63.79, 64.27, 64.78, 65.3, 65.8, 66.27, 66.8, 67.3, 67.8, 68.31, 68.78, 69.3, 69.8, 70.32, 70.81, 71.32, 71.81, 72.33, 72.82, 73.31, 73.83, 74.33, 74.82, 75.32, 75.83, 76.34, 76.84, 77.35, 77.82, 78.34, 78.85, 79.36, 79.84, 80.35, 80.85, 81.36, 81.86, 82.37, 82.86, 83.37, 83.88, 84.36, 84.88, 85.38, 85.88, 86.38, 86.89, 87.38, 87.89, 88.39, 88.89, 89.4, 89.9, 90.39, 90.9, 91.4, 91.91, 92.37, 92.89, 93.4, 93.91, 94.41, 94.91, 95.42), Absorbance = c(1.401351929, 1.403320313, 1.405181885, 1.406326294, 1.407440186, 1.409118652, 1.410095215, 1.410797119, 1.411560059, 1.412918091, 1.413970947, 1.414245605, 1.416000366, 1.415435791, 1.41809082, 1.4190979, 1.419677734, 1.420150757, 1.421966553, 1.420333862, 1.422637939, 1.422790527, 1.423461914, 1.426513672, 1.426315308, 1.426071167, 1.426467896, 1.428710938, 1.428070068, 1.428817749, 1.429733276, 1.432144165, 1.432434082, 1.433227539, 1.434616089, 1.435806274, 1.434814453, 1.436096191, 1.436096191, 1.436447144, 1.437896729, 1.4375, 1.438934326, 1.440139771, 1.440139771, 1.441741943, 1.442108154, 1.443969727, 1.444778442, 1.443862915, 1.444534302, 1.445648193, 1.444473267, 1.446395874, 1.447219849, 1.446151733, 1.449569702, 1.449066162, 1.448852539, 1.4503479, 1.451385498, 1.45111084, 1.451217651, 1.453125, 1.452560425, 1.455047607, 1.455093384, 1.456665039, 1.457977295, 1.457336426, 1.458648682, 1.46043396, 1.462158203, 1.464813232, 1.463531494, 1.468048096, 1.468643188, 1.470748901, 1.471878052, 1.476257324, 1.478057861, 1.482040405, 1.484466553, 1.486129761, 1.48815918, 1.496520996, 1.499786377, 1.504302979, 1.507217407, 1.512985229, 1.517471313, 1.524108887, 1.528198242, 1.534637451, 1.539169312, 1.546142578, 1.554611206, 1.55809021, 1.56854248, 1.572875977, 1.580307007, 1.585739136, 1.592514038, 1.600067139, 1.609222412, 1.616607666, 1.622375488, 1.631469727, 1.635635376, 1.642929077, 1.649780273, 1.655014038, 1.661483765, 1.663742065, 1.671859741, 1.677200317, 1.677108765, 1.683380127, 1.684082031, 1.687438965, 1.694595337, 1.694961548, 1.696685791, 1.696685791, 1.699768066, 1.702514648, 1.703613281, 1.705093384, 1.70022583, 1.707595825, 1.707962036, 1.709075928, 1.705276489, 1.71055603, 1.709259033, 1.70916748, 1.709732056, 1.710189819, 1.710281372, 1.711868286, 1.711883545, 1.713104248, 1.713760376, 1.711120605, 1.709716797, 1.711776733, 1.712814331, 1.714324951, 1.711120605, 1.713378906, 1.712432861, 1.716125488, 1.710006714, 1.710845947, 1.711502075, 1.711120605, 1.710006714, 1.70980835, 1.708602905, 1.708236694, 1.710189819, 1.707672119, 1.706939697, 1.710006714, 1.706192017, 1.706573486, 1.706207275, 1.705734253, 1.706207275, 1.705184937, 1.70954895, 1.705841064, 1.702972412, 1.703979492, 1.703063965, 1.709350586, 1.703338623, 1.700408936, 1.705276489, 1.705368042)), row.names = 1621:1800, class = "data.frame")

Code For my Attempt

raw = "<insert dput line>>"                                                                                              
columns = c("Temperature","Absorbance")
first = data.frame(matrix(nrow=0,ncol=2))
colnames(dFrame) = columns

for (i in 1:nrow(raw)) {
  if(i != nrow(raw)) {
    cAbs = raw[i,2]
    nextAbs = raw[i 1,2]
    cT = raw[i,1]
    nextT = raw[i 1,1]
    Temperature = raw[i,1]
    Absorbance =((nextAbs-cAbs)/(nextT-cT))
    
    t <- data.frame(Temperature,Absorbance)
    names(t) <- names(raw)
    first <- rbind(first, t)
  }
}

ggplot() 
  geom_point(data=raw, aes(x=Temperature,y=Absorbance), color = "red")  
  geom_point(data = first, aes(x=Temperature,y = Absorbance), color = "blue")

What I was expecting I was expecting an output that had the shape of something like so: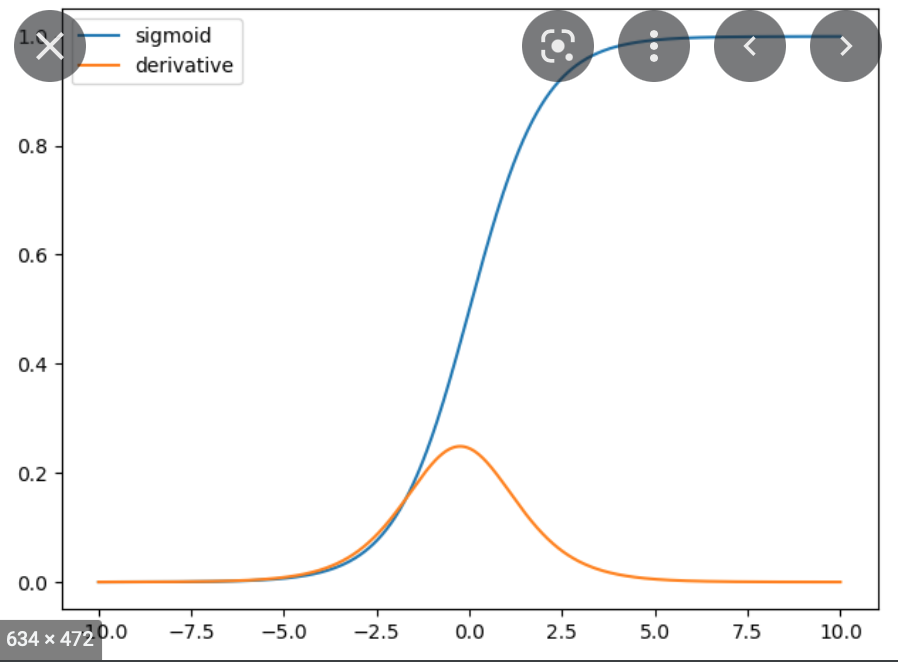

CodePudding user response：

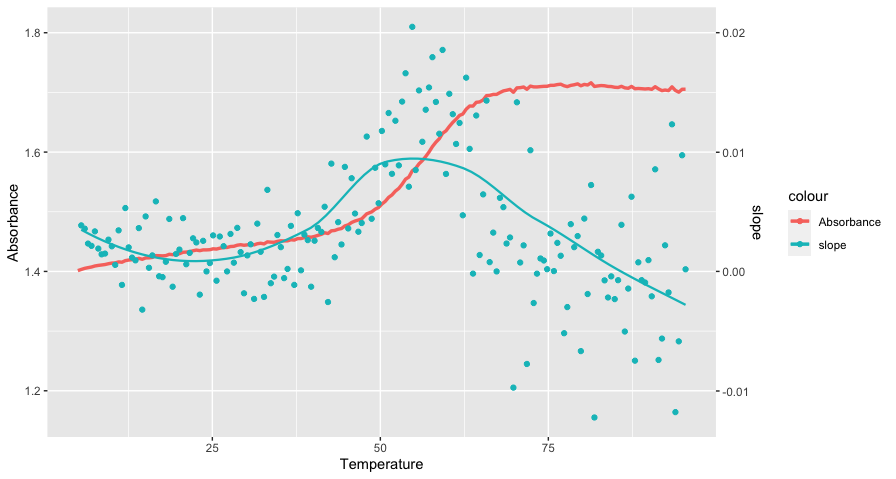
library(dplyr); library(ggplot2)
df %>%
  arrange(Temperature) %>%
  mutate(slope = (Absorbance - lag(Absorbance))/
                 (Temperature - lag(Temperature))) %>%
  ggplot(aes(Temperature))  
  geom_line(aes(y= Absorbance, color = "Absorbance"), size = 1.2)  
  geom_point(aes(y= slope * 20   1.4, color = "slope"))  
  geom_smooth(aes(y= slope * 20   1.4, color = "slope"), se = FALSE, size = 0.8)  
  scale_y_continuous(sec.axis = sec_axis(trans = ~(.x - 1.4)/20, name = "slope"))

CodePudding user response：

If the data is even a little noisy, calculating the derivative by first differencing can be very noisy.

You can get a better estimate by fitting a smoothing spline function and calculating the derivative of the spline function. By differentiating a smooth function, you get a smooth derivative.

In most cases, smooth.spline with default arguments is fine, but I recommend taking a look at the result and possibly tuning the smooth.spline parameters for more or less smoothing, depending on your judgment.

edit: I learned this approach from the Numerical Recipes textbook.

library(tidyverse)

df <- tibble(
  x = seq(1, 15, by = 0.1),
  y = sin(x)   runif(length(x), -0.2, 0.2),
  d1_diff = c(NA, diff(y) / diff(x)),
  d1_spline = smooth.spline(x, y) %>% predict(x, deriv = 1) %>% pluck("y")
)

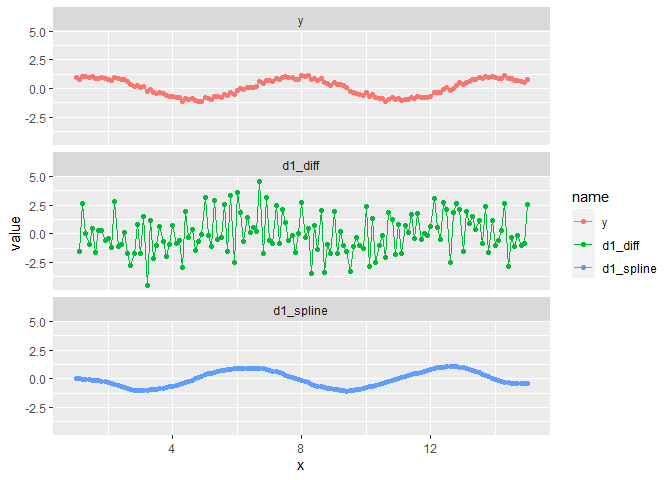
df %>%
  pivot_longer(-x) %>%
  mutate(name = factor(name, unique(name))) %>%
  ggplot()   aes(x, value, color = name)   geom_point()   geom_line()  
  facet_wrap(~name, ncol = 1)
#> Warning: Removed 1 rows containing missing values (geom_point).
#> Warning: Removed 1 row(s) containing missing values (geom_path).

^{Created on 2022-10-26 with reprex v2.0.2}