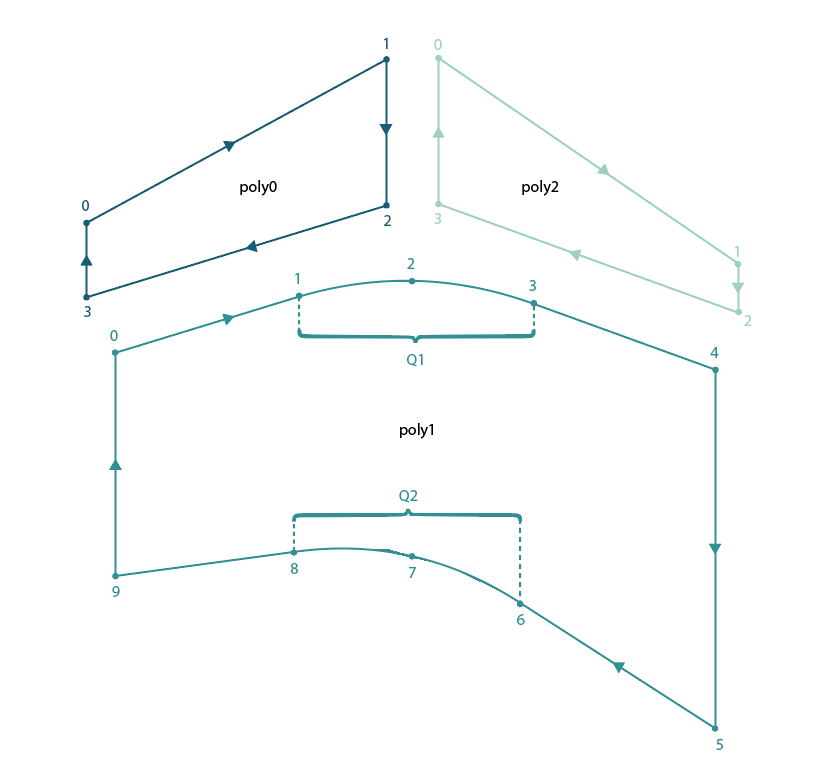
There is an SVG elements with few paths (polygons) having adjacent sides.

<svg id="dummyIn" viewBox="0 0 800 800" preserveAspectRatio="xMinYMin meet">
    <path id="poly0" d="M200 296.6L400 187.6L400 285L200 346.2Z" fill="#005f73" />
    <path id="poly1" d="M200 346.2L320 309.48 Q400 285 478.6533272400307 313.51183112451116L600 357.5L600 596.7L467.8848705014076 511.6839141676558 Q400 468 320 478.8L200 495Z" fill="#0a9396" />
    <path id="poly2" d="M400 187.6L600 324.8L600 357.5L400 285Z" fill="#94d2bd" />
</svg>

The path named 'poly1' have two curves segments based on Q command L320 309.48 Q400 285 478.6533272400307 313.51183112451116 and L467.8848705014076 511.6839141676558 Q400 468 320 478.8L200 495.

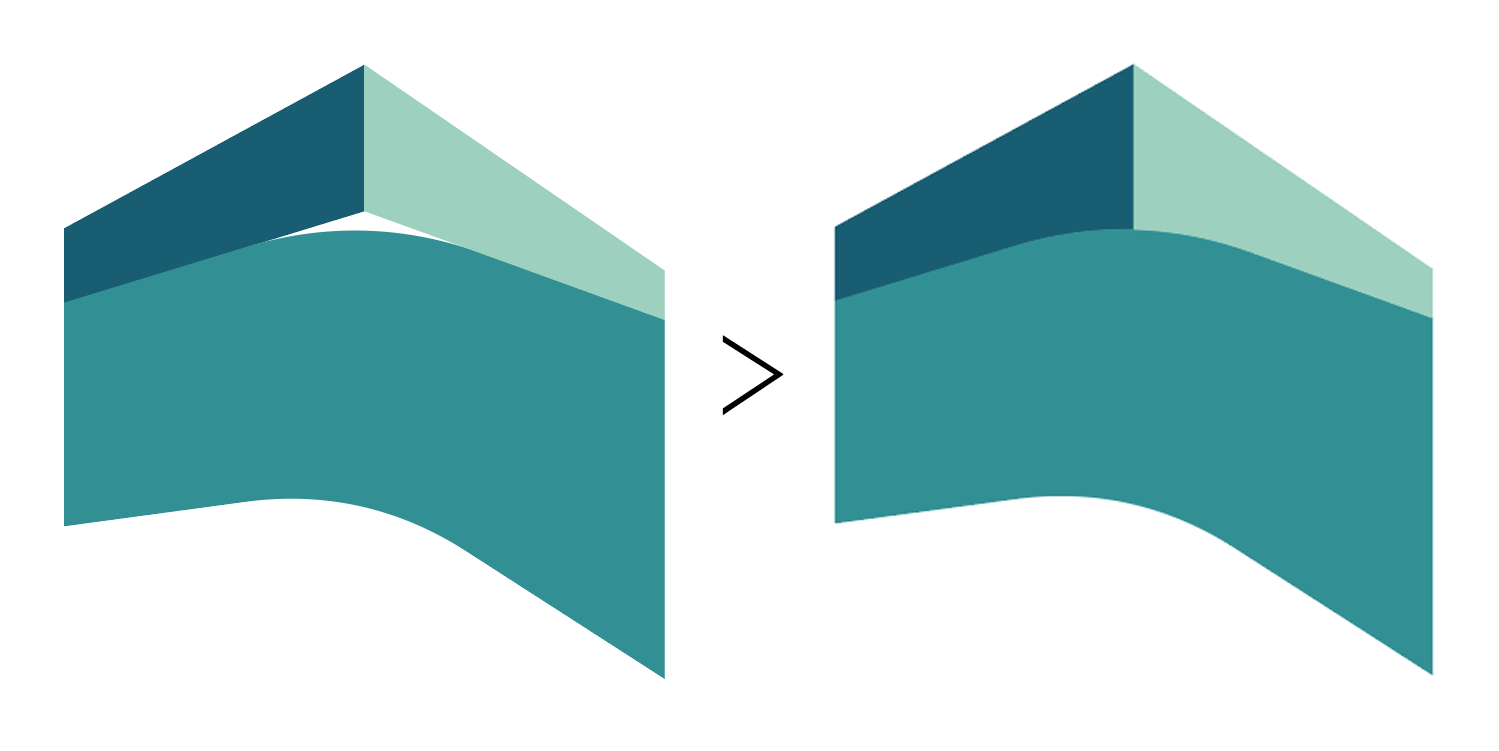
The task is to recalculate these segments in JavaScript for 'poly0' and 'poly2' in a way, so the output would be

Did an output mock-up in Adobe Illustrator by cutting these curves into segments and the output SVG is

<svg id="dummyOut" viewBox="0 0 800 800" preserveAspectRatio="xMinYMin meet">
    <path id="poly0" d="M200 296.6L400 187.6L478.7,313.5c-26.1-9.5-52.3-14.5-78.7-15.3L200 346.2Z" fill="#005f73" />
    <path id="poly1" d="M200 346.2L320 309.48 Q400 285 478.6533272400307 313.51183112451116L600 357.5L600 596.7L467.8848705014076 511.6839141676558 Q400 468 320 478.8L200 495Z" fill="#0a9396" />
    <path id="poly2" d="M400 187.6L600 324.8L600 357.5L478.7,313.5c-26.1-9.5-52.3-14.5-78.7-15.3Z" fill="#94d2bd" />
</svg>

In other words, the goal is to split L320 309.48 Q400 285 478.6533272400307 313.51183112451116 into two parts L400,298.3c-26.6-0.7-53.2,3-80,11.2 and L478.7,313.5c-26.1-9.5-52.3-14.5-78.7-15.3.

That's just an Illustrator solution based on C commands. But it is not obligatory.

CodePudding user response：

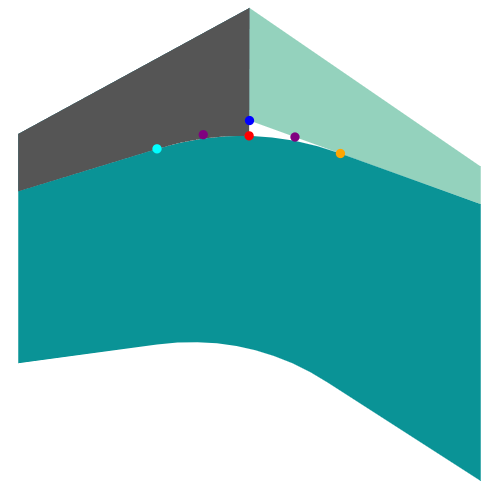
You just need to calculate some interpolated points.

• cyan: last point from previous command (preceding Q)
• blue: Q quadratic bézier control point
• orange: Q command end point
• purple1 2: middle points between cyan-blue and blue-orange – these will become the new Q control points
• red: middle point between purple1-purple2 – will become the new L command point.

let p0 = [320, 309.48];
let p1 = [478.653, 313.512];
let cp1 = [400, 285];
renderPoint(svg, p0, 'cyan')
renderPoint(svg, p1, 'orange')
renderPoint(svg, cp1, 'blue')

let m1 = interpolatedPoint(p0, cp1);
let m2 = interpolatedPoint(cp1, p1);
renderPoint(svg, m1, 'purple')
renderPoint(svg, m2, 'purple')

let p2 = interpolatedPoint(m1, m2);
renderPoint(svg, p2, 'red');

//new segment
let d0 = `
M 200 296.6
L 400 187.6
L ${p2.x} ${p2.y}
Q ${m1.x} ${m1.y} ${p0.x} ${p0.y}
L200 346.2
`;

poly0.setAttribute('d', d0)

let d1 = `
M 400 187.6 
L 600 324.8
L 600 357.5
L ${p1.x} ${p1.y}
Q ${m2.x} ${m2.y} ${p2.x} ${p2.y}
z
`;

poly2.setAttribute('d', d1)





/**
 * Linear  interpolation (LERP) helper
 */
function interpolatedPoint(p1, p2, t = 0.5) {
    //t: 0.5 - point in the middle
    if (Array.isArray(p1)) {
        p1.x = p1[0];
        p1.y = p1[1];
    }
    if (Array.isArray(p2)) {
        p2.x = p2[0];
        p2.y = p2[1];
    }
    let [x, y] = [(p2.x - p1.x) * t   p1.x, (p2.y - p1.y) * t   p1.y];
    return {
        x: x,
        y: y
    };
}


/**
 * render point
 * accepts coordinate array and point object
 **/
function renderPoint(svg, coords, fill = "red", r = "0.5%") {
    if (Array.isArray(coords)) {
        coords = {
            x: coords[0],
            y: coords[1]
        };
    }
    let marker = `<circle cx="${coords.x}" cy="${coords.y}" r="${r}" fill="${fill}">
      <title>${coords.x} ${coords.y}</title></circle>`;
    svg.insertAdjacentHTML("beforeend", marker);
}

<svg id="svg" viewBox="0 0 800 800" >
    <path id="poly0" d="M200 296.6L400 187.6L400 285L200 346.2Z" fill="#005f73" />
    <path id="poly2" d="M400 187.6L600 324.8L600 357.5L400 285Z" fill="#94d2bd" />
    <path id="poly1" d="
M 200 346.2 
L 320 309.48 
Q 400 285  478.653 313.512
L 600 357.5 
L 600 596.7 
L 467.885 511.684
Q 400 468  320 478.8
L200 495Z" fill="#0a9396" />
</svg>

You don't really need the LERP (linear interpolation) helper method (but it's quite handy).
You can just get the middle points like so:

m1 = {x:(x1 x2)/2, y:(y1 y2)/2}  

BTW, splitting cubic béziers works similarly:
You just need more interpolations.
See this excellent post: The Anatomy Of A Cubic Bézier Curve In SVG