How to depict a graph of an implicit differentiation equation on R?-CodePudding

I'm now learning about calculus and want to depict a graph of x^2 6x y^4 = 7, which I can using online graphing tool desmos.

But when I'm not sure how this is achievable on R. The first thing I thought is convert it in a form of y = f(x), but return (x^2 6*x - 7)^(1/4) gave me a different result.

At the same time, it seems impossible to return a equation in a function (return (x^2 6*x y^4 = 7)). So how can I depict it on R?

Here is a sample code I usually use to depict a continuous graph.

f <- function(x) {
  return () # return an equation
}

ggplot(data.frame(x=seq(-10,10,length.out=10)), aes(x))   stat_function(fun=f)

CodePudding user response：

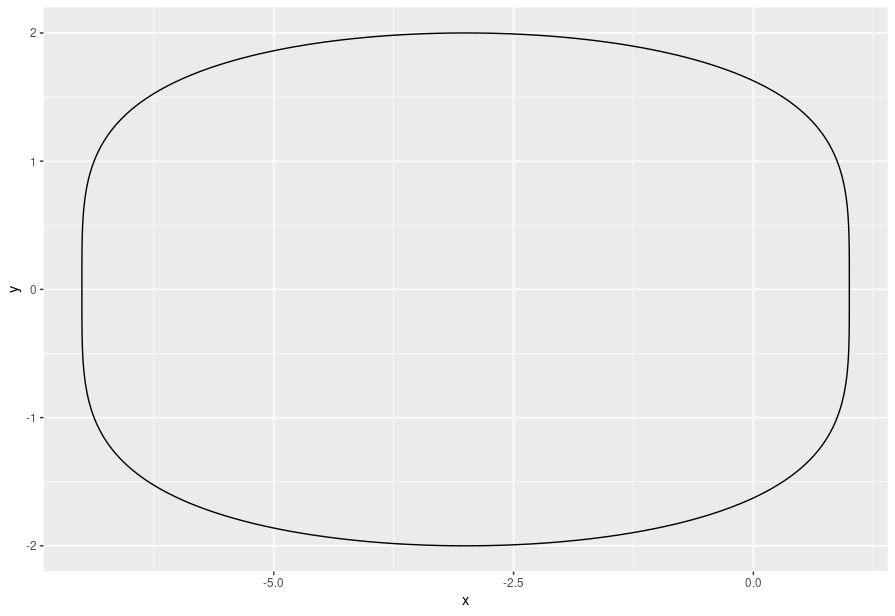
You can use contourLines:

f <- function(x,y) x^2   6*x   y^4

x <- seq(-10, 3, len = 200)
y <- seq(-3, 3, len = 200)
z <- outer(x, y, f)
cr <- contourLines(x, y, z, levels = 7)

plot(cr[[1]]$x, cr[[1]]$y, type = "l")

library(ggplot2)
dat <- data.frame(x = cr[[1]]$x, y = cr[[1]]$y)
ggplot(dat)   geom_path(aes(x, y))

CodePudding user response：

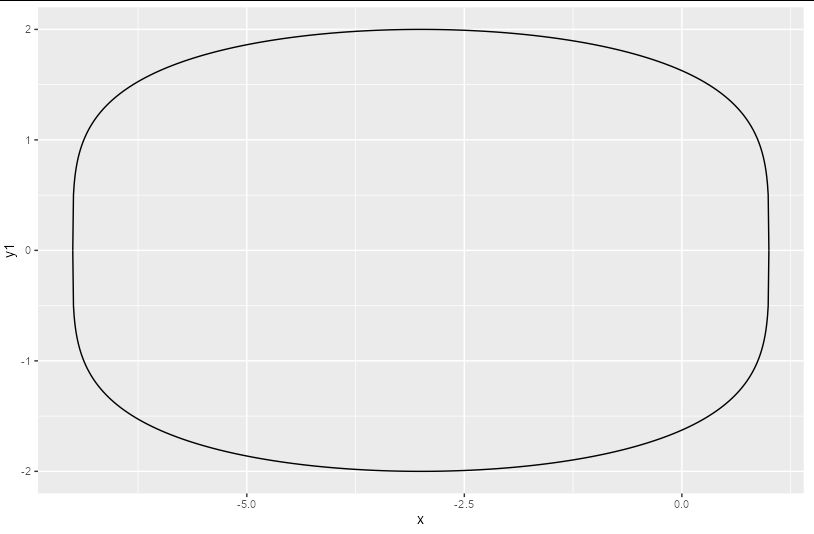
You can have separate functions for the positive and negative solutions for y

f1 <- function(x) (7 - x^2 - 6*x)^(1/4)

f2 <- function(x) -f1(x)

Now just create a vector each for positive and negative values along the domain of x:

x <- seq(-7, 1, length = 1000)
y1 <- f1(x)
y2 <- f2(x)

And plot:

ggplot()   
  geom_line(aes(x, y1))   
  geom_line(aes(x, y2))