How to detect circle defects?-CodePudding

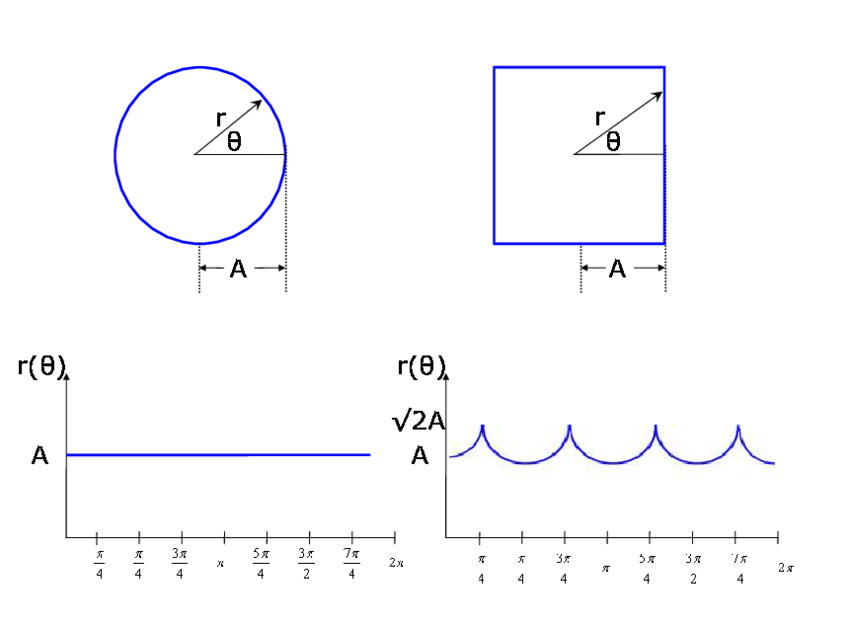
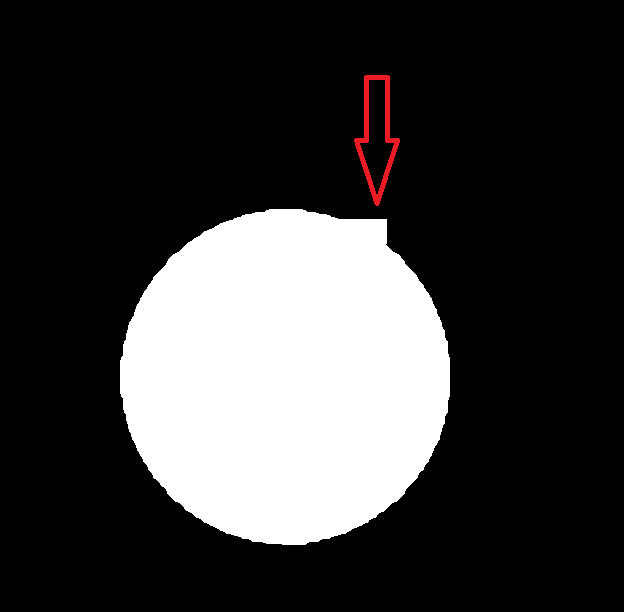
Is there any way to tell if a circle has such defects? Roundness does not work. Or is there a way to eliminate them?

enter image description here

    perimeter = cv2.arcLength(cnts[0],True)
    area = cv2.contourArea(cnts[0])
    roundness = 4*pi*area/(perimeter*perimeter)
    print("Roundness:", roundness)

CodePudding user response：

The "roundness" measure is sensitive to a precise estimate of the perimeter. What cv2.arcLength() does is add the lengths of each of the polygon edges, which severely overestimates the length of outlines. I think this is the main reason that this measure hasn't worked for you. With a better perimeter estimator you would get useful results.

An alternative measure that might be more useful is "circularity", defined as the coefficient of variation of the radius. In short, you compute the distance of each polygon vertex (i.e. outline point) to the centroid, then determine the coefficient of variation of these distances (== std / mean).

I wrote a quick Python script to compute this starting from an OpenCV contour:

import cv2
import numpy as np

# read in OP's example image, making sure we ignore the red arrow
img = cv2.imread('jGssp.png')[:, :, 1]
_, img = cv2.threshold(img, 127, 255, 0)

# get the contour of the shape
contours, hierarchy = cv2.findContours(img, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_NONE)
contour = contours[0][:, 0, :]

# add the first point as the last, to close it
contour = np.concatenate((contour, contour[0, None, :]))

# compute centroid
def cross_product(v1, v2):
    """2D cross product."""
    return v1[0] * v2[1] - v1[1] * v2[0]

sum = 0.0
xsum = 0.0
ysum = 0.0
for ii in range(1, contour.shape[0]):
    v = cross_product(contour[ii - 1, :], contour[ii, :])
    sum  = v
    xsum  = (contour[ii - 1, 0]   contour[ii, 0]) * v
    ysum  = (contour[ii - 1, 1]   contour[ii, 1]) * v

centroid = np.array([ xsum, ysum ]) / (3 * sum)

# Compute coefficient of variation of distances to centroid (==circularity)
d = np.sqrt(np.sum((contour - centroid) ** 2, axis=1))
circularity = np.std(d) / np.mean(d)

CodePudding user response：

This make me think of a similar problem that I had. You could compute the signature of the shape. The signature can be defined as, for each pixel of the border of the shape, the distance between this pixel and the center of the shape.

For a perfect circle, the distance from the border to the center should be constant (in an ideal continuous world). When defects are visible on the edge of the circle (either dents or excesses), the ideal constant line changes to a wiggly curve, with huge variation when on the defects.

It's fairly easy to detect those variation with FFT for example, which allows to quantify the defect significance.

You can expand this solution to any given shape. If your ideal shape is a square, you can compute the signature, which will give you some kind of sinusoidal curve. Defects will appear in a same way on the curve, and would be detectable with the same logic as with a circle.

I can't give you an code example, as the project was for a company project, but the idea is still here.