sampling from a CDF only in R?-CodePudding

I have the following function below

I'd like to sample from this CDF (x values) but can't find the inverse function by hand. Is there a way to do it in R?

a <- 3.1
be <- -0.15
ga <- 0.78
delt <- 0.12

c<- 3.5

b <- exp(a be*c*(1 c))
g <- exp((ga delt*c)*c)


flc_F <- function(x){
  #x between 0 and 1
  if (x<1){
    return ((b*(g-1)*(1-b^x))/(b*(g-1) (1-b*g)*b^x))
  } else {
    return (1)
  }
}

CodePudding user response：

You can create an inverse with uniroot:

a <- 3.1
be <- -0.15
ga <- 0.78
delt <- 0.12

c<- 3.5

b <- exp(a be*c*(1 c))
g <- exp((ga delt*c)*c)


flc_F <- function(x){
  #x between 0 and 1
  if (x<1){
    return ((b*(g-1)*(1-b^x))/(b*(g-1) (1-b*g)*b^x))
  } else {
    return (1)
  }
}
flc_F <- Vectorize(flc_F)

# Quantile function
Qflc_F <- function(p){
  sapply(p, function(.x) uniroot(
        function(p) flc_F(p) - .x, 
        interval = c(0, 1e16) 
  )[["root"]])
}

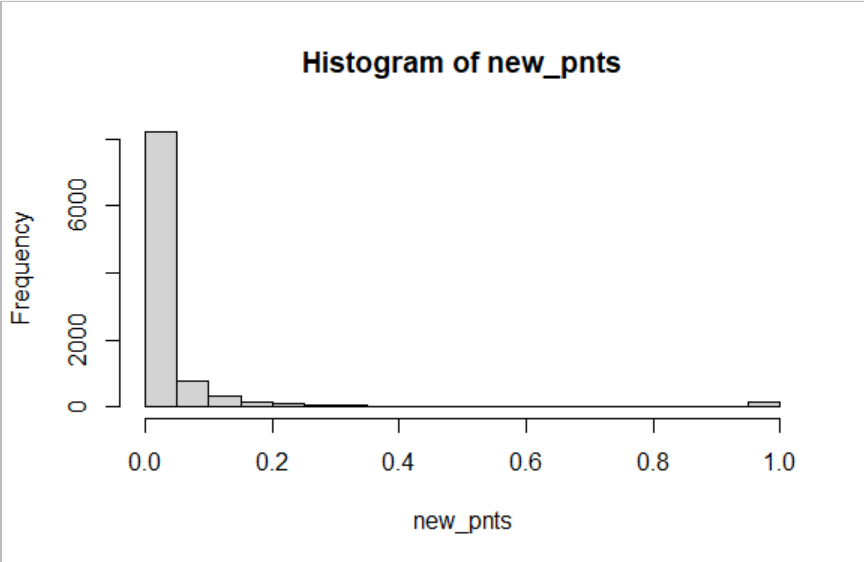
Plot of the functions. CDF...

curve(flc_F(x), from = 0, to = 1)

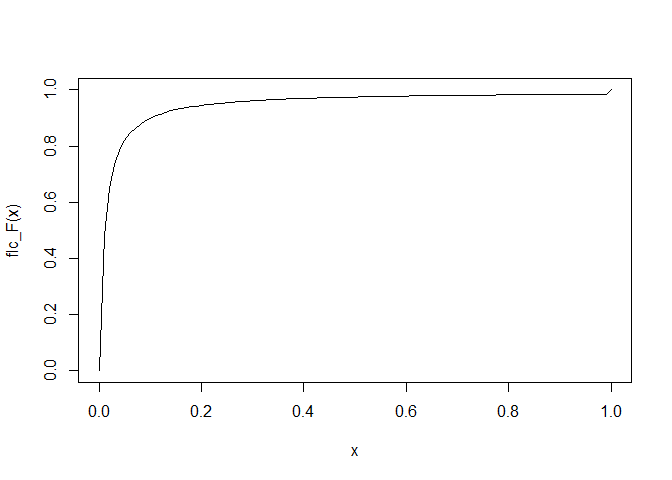
And Inverse (that is, Quantile function:

curve(Qflc_F(x), from = 0.1, to = 0.99)

PD: Note two things: 1 - I vectorized your original function using Vectorize(), thus you can use it with vectors (there are possibly more efficient ways though) 2 - I set a limit for search the root in uniroot between 0 and 1e16, of course that function could be refined to treat Inf values in better way.

CodePudding user response：

Since you said you have the cdf, You can use the inverse cdf method to sample from the density:

a <- 3.1
be <- -0.15
ga <- 0.78
delt <- 0.12

c<- 3.5

b <- exp(a be*c*(1 c))
g <- exp((ga delt*c)*c)


flc_F <- function(x){
  #x between 0 and 1
  if(x<0) return(NA)
  if (x<1){
    return ((b*(g-1)*(1-b^x))/(b*(g-1) (1-b*g)*b^x))
  } else {
    return (1)
  }
}

# Inverse of the cdf:

flc_Inv <- function(x)optimise(\(y)(flc_F(y)-x)^2,c(0,1) )[[1]]

Now just sample points from uniform(0,1) and invert them to follow the said distribution using the inverse cdf function:

 pnts <- runif(10000) 
 new_pnts <- sapply(pnts, flc_Inv)

Now you can use the function below to sample:

 r_flc <- function(n) sapply(runif(n), flc_Inv)
 hist(r_flc(10000))