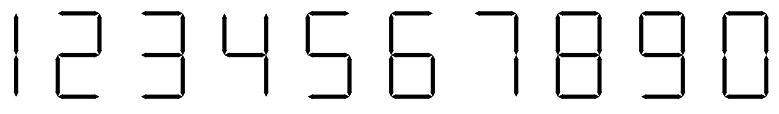I'm having trouble finding the smallest number possible from the following question:

Matchsticks are ideal tools to represent numbers. A common way to represent the ten decimal digits with matchsticks is the following:

This is identical to how numbers are displayed on an ordinary alarm clock. With a given number of matchsticks you can generate a wide range of numbers. We are wondering what the smallest and largest numbers are that can be created by using all your matchsticks.

Input:

On the first line one positive number: the number of testcases, at most 100. After that per testcase:

One line with an integer n (2 <= n <= 100): the number of matchsticks you have.

Output:

Per testcase:

One line with the smallest and largest numbers you can create, separated by a single space. Both numbers should be positive and contain no leading zeroes.

I've tried multiple different ways to try to solve this problem, I'm currently trying to:

1. find the minimal number of digits needed for the smallest number
2. send digit to a function minimum() which should generate all the different combinations of numbers that are the length of digits. I want to store all these numbers in a list and then take min() to get the smallest one. I'm not getting this part to work, and would appreciate some inspiration.

Something to remember is that the number can't start with a 0.

CodePudding user response：

if 2 <= n <= 100:
    value = (n 6)//7

Unless I'm mistaken, this should work for part 2 (added a fix for 17, 24...):

numdict = {2:1,3:7,4:4,5:2,6:0,7:8,8:10,9:18,10:22,11:20,12:28,13:68}

def min_stick(n):
    if 2 <= n <= 13:
        return numdict[n]
    digits = (n   6) // 7
    base = str(numdict[7 n%7])
    if base == '22':
        base = '200'
    return int(base "8"*(digits - len(base)))

And, though this one's a no-brainer:

def max_stick(n):
    if n%2:
        return int("7" "1"*((n-3)//2))
    return int("1"*(n//2))

Ok, so just for the sake of it, I coded what you asked: a recursive function that returns all possible combinations with n matchsticks.

stick = {0:6,1:2,2:5,3:5,4:4,5:5,6:6,7:3,8:7,9:6}

def decompose(n):
    retlist = []    
    if n==0:
        return [""]
    for i in stick:
        if (left := n-stick[i]) >1 or left == 0:
            retlist  = [str(i) el for el in decompose(left)]
    return retlist

def extr_stick(n):
    purged_list = [int(i) for i in decompose(n) if not i.startswith('0')]
    return min(purged_list), max(purged_list)

It becomes slow when n grows, but anyway...

extr_stick2(30)
Out[18]: (18888, 111111111111111)