plotting triangle inside circle-CodePudding

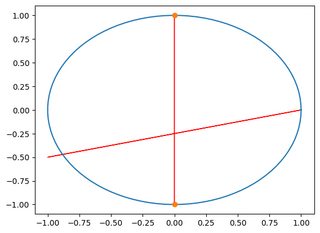
I am creating a circle and want to then develop a right-angle triangle, or any isometric form of a triangle. Whereby, I can take any line distance between two edges of the circle and draw arrows toward the peak point.

For example:

import numpy as np
import matplotlib.pyplot as plt
import math

theta = np.linspace(0, 2*np.pi, 100)
x1 = np.cos(theta) 
y1 = np.sin(theta) 

plt.plot(x1, y1)
for i in [min(y1), max(y1)]:
    plt.plot(0, i, '-ok', mfc='C1', mec='C1')
plt.arrow(0,min(y1),0,2*max(y1),width=0.001,color='red',head_starts_at_zero=False)
plt.arrow(min(x1), (1/2)*min(y1), 2*max(x1), (1/2)*max(y1),width=0.001,color='red',head_starts_at_zero=False)

However, I cannot accurately get the distance between two points correct when i aim for any form of a triangle.

However, I can easily achieve it when setting y to 0 in the second arrow. Perhaps there is a general equation to do this?

CodePudding user response：

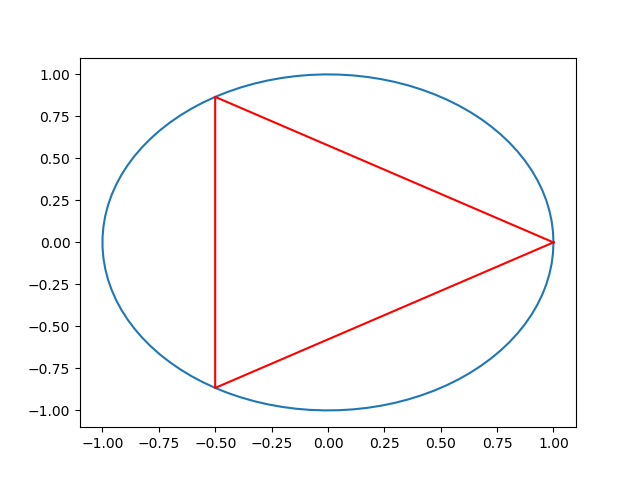
Like this:

import numpy as np
import matplotlib.pyplot as plt
import math

theta = np.linspace(0, 2*np.pi, 100)
x1 = np.cos(theta) 
y1 = np.sin(theta) 

plt.plot(x1, y1)

x = np.array([0,120,240,0])
y = np.array([0,120,240,0])
x = np.cos( x * np.pi / 180 )
y = np.sin( y * np.pi / 180 )

plt.plot( x, y, color='red' )
plt.show()

Output:

In fact, if you choose ANY three angles, you'll get an inscribed triangle.