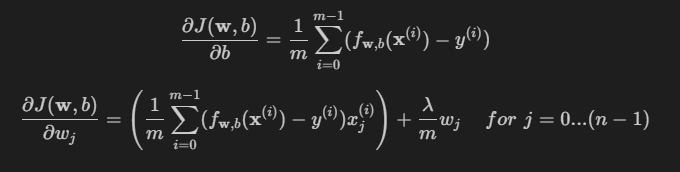VSCode not rendering Markdown with latex in Jupyter notebook-CodePudding

The following Markdown code from a Jupyter notebook produces an error in VSCode. Some initial googling suggests this has to do with Latex rendering in markdown in vscode? Any suggetions on how to fix it, whether it's a VSCode setting, a VSCode extension, or something else? For what it's worth, the equation renders just fine in a browser (i.e., outside of VSCode).

<a name="3.5"></a>
### 3.5 Gradient for regularized logistic regression

In this section, you will implement the gradient for regularized logistic regression.


The gradient of the regularized cost function has two components. The first, $\frac{\partial J(\mathbf{w},b)}{\partial b}$ is a scalar, the other is a vector with the same shape as the parameters $\mathbf{w}$, where the $j^\mathrm{th}$ element is defined as follows:

$$\frac{\partial J(\mathbf{w},b)}{\partial b} = \frac{1}{m}  \sum_{i=0}^{m-1} (f_{\mathbf{w},b}(\mathbf{x}^{(i)}) - y^{(i)})  $$

$$\frac{\partial J(\mathbf{w},b)}{\partial w_j} = \left( \frac{1}{m}  \sum_{i=0}^{m-1} (f_{\mathbf{w},b}(\mathbf{x}^{(i)}) - y^{(i)}) x_j^{(i)} \right)   \frac{\lambda}{m} w_j  \quad\, \mbox{for $j=0...(n-1)$}$$

CodePudding user response：

I could reproduce your error...\mbox{} seems to be problematic. Under the assumption, that you are using \mbox for the correct spacing, there is a simple alternative to fix it. \, creates a half space width... The following code should do the trick:

In this section, you will implement the gradient for regularized logistic regression.


The gradient of the regularized cost function has two components. The first, $\frac{\partial J(\mathbf{w},b)}{\partial b}$ is a scalar, the other is a vector with the same shape as the parameters $\mathbf{w}$, where the $j^\mathrm{th}$ element is defined as follows:

$$\frac{\partial J(\mathbf{w},b)}{\partial b} = \frac{1}{m}  \sum_{i=0}^{m-1} (f_{\mathbf{w},b}(\mathbf{x}^{(i)}) - y^{(i)})  $$  

$$\frac{\partial J(\mathbf{w},b)}{\partial w_j} = \left( \frac{1}{m}  \sum_{i=0}^{m-1} (f_{\mathbf{w},b}(\mathbf{x}^{(i)}) - y^{(i)}) x_j^{(i)} \right)   \frac{\lambda}{m} w_j  \quad\, for\,\,j=0...(n-1)$$

for\,\,j=0...(n-1)

With the result...

Hope this fix helps. I am still looking for an explaination though