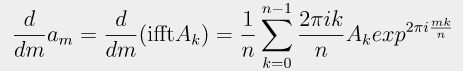Scaling issue taking derivative in frequency domain and transforming back to time using numpy fft-CodePudding

I am trying to take the derivative of a signal in the frequency domain using numpy. For a continuous signal this is just a multiplication of the spectrum by 2*pi*i*f.

For a discrete signal, considering the numpy FFT implementation, I thought it would be this:

i.e. a multiplication of the FFT by 2*pi*i*k/n

But it's not: the division by n is not required.

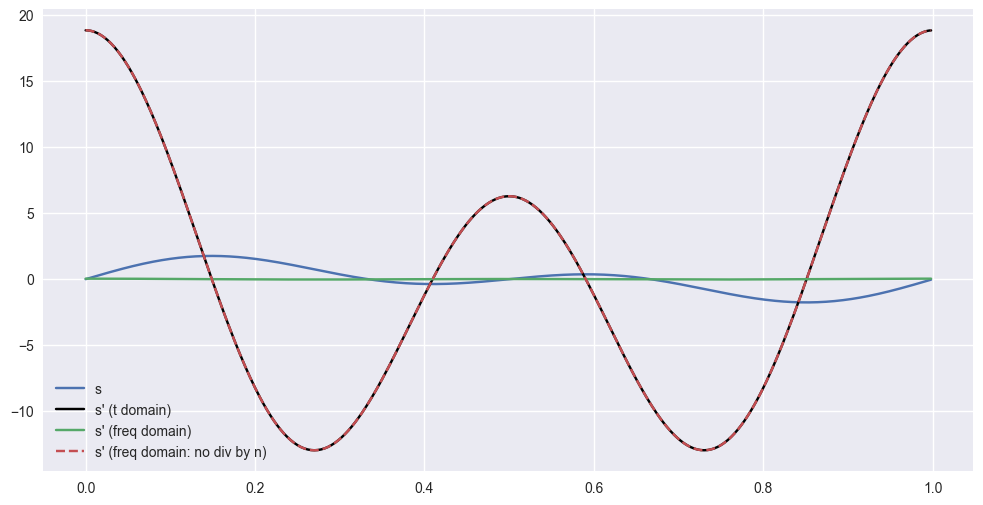
This is shown in the plot below: compare the green curve (with division by n) to the red-dashed curve (no division by n). I plotted the time domain derivative in black as a sanity check.

Why is the division by n not required? I feel I'm missing something obvious but can't figure it out. Have I made a silly math error that I can't see, or perhaps my understanding of numpy implementation of the DFT is incorrect?

(I'm only dealing with real input and thus using rfft/irfft, but i've tested with fft/ifft and have the same result.)

Here's my test code.

import numpy as np
import matplotlib.pyplot as plt
plt.style.use('seaborn')

def sin(t, amp, freq):
    return amp * np.sin(2 * np.pi * freq * t)

dt = 0.002
t = np.arange(0,1,dt)
n = len(t)              # n is even

s = sin(t, 1, 1)   sin(t, 1, 2)
ds_grad = np.gradient(s, dt)    # time derivative

S = np.fft.rfft(s)
freqs = np.fft.rfftfreq(n, dt)

dS = np.ones(len(S), dtype='complex')    # freq derivative
for i in np.arange(len(dS)):
    dS[i] = 1/n * 2* np.pi * 1j * freqs[i] * S[i]
ds = np.fft.irfft(dS)

dS_ = np.ones(len(S), dtype='complex')    # freq deriv without 1/n
for i in np.arange(len(dS_)):
    dS_[i] = 2 * np.pi * 1j * freqs[i] * S[i]
ds_ = np.fft.irfft(dS_)

plt.figure(figsize=(12,6))
plt.plot(t, s, label='s')
plt.plot(t, ds_grad, 'k', label='s\' (t domain)')
plt.plot(t, ds, label='s\' (freq domain)' )
plt.plot(t, ds_, '--', label='s\' (freq domain: no div by n)' )
plt.legend(loc='lower left')
plt.show()

CodePudding user response：

The multiplication by 2*pi*i*k/n is correct for a time-domain signal sampled at integer positions (ie the signal is s[i] for i=0..n-1). If you want to take the sample locations into account, you have to additionally divide by dt, which in your case happens to be equivalent to multiplying by n.