Calculate acceleration and deceleration while traveling from A to B-CodePudding

I am using code like the example below to simulate travel from one point to another.

The goal I want to achieve is have a realistic acceleration and deceleration at the beginning and end of trip regardless of the length of trip, while in the middle of the trip be going at max speed.

I want to make it so if the trip is short enough that the traveler never reaches max speed, they will merely speed up to midpoint of trip, then decelerate. This is necessary as this code will be used for travel between various distances.

import time

meters = 100000
traveling = True
meters_second = 0
max_meters_second = 1000
seconds = 0

while traveling:
    if meters <= 0:
        traveling = False
        meters = 0
        meters_second = 0
        seconds = 0
        print('you have arrived!')
    else:
        if seconds < 20:
            meters_second  = 1
        elif meters < 10000:
            meters_second -= 1
        else:
            meters_second = max_meters_second
        meters -= meters_second
        seconds  = 1
        print(f'dist to destination(m):{meters} M/s: {meters_second} time passed(s):{seconds}')
        time.sleep(1)

With this example, there is a sort of constant acceleration and deceleration at beginning and end of trip, but it doesn't work right.

This may be more of a math problem, but there's probably a variable I can include to make this easier that I am missing.

The output of current code:

meters to dest:99999 M/s: 1 time elapsed(s):1
meters to dest:99997 M/s: 2 time elapsed(s):2
meters to dest:99994 M/s: 3 time elapsed(s):3
meters to dest:99990 M/s: 4 time elapsed(s):4
meters to dest:99985 M/s: 5 time elapsed(s):5
meters to dest:99979 M/s: 6 time elapsed(s):6
meters to dest:99972 M/s: 7 time elapsed(s):7
meters to dest:99964 M/s: 8 time elapsed(s):8
meters to dest:99955 M/s: 9 time elapsed(s):9
meters to dest:99945 M/s: 10 time elapsed(s):10
meters to dest:99934 M/s: 11 time elapsed(s):11
meters to dest:99922 M/s: 12 time elapsed(s):12
meters to dest:99909 M/s: 13 time elapsed(s):13
meters to dest:99895 M/s: 14 time elapsed(s):14
meters to dest:99880 M/s: 15 time elapsed(s):15
meters to dest:99864 M/s: 16 time elapsed(s):16
meters to dest:99847 M/s: 17 time elapsed(s):17
meters to dest:99829 M/s: 18 time elapsed(s):18
meters to dest:99810 M/s: 19 time elapsed(s):19
meters to dest:99790 M/s: 20 time elapsed(s):20
meters to dest:98790 M/s: 1000 time elapsed(s):21
meters to dest:97790 M/s: 1000 time elapsed(s):22
meters to dest:96790 M/s: 1000 time elapsed(s):23
meters to dest:95790 M/s: 1000 time elapsed(s):24
meters to dest:94790 M/s: 1000 time elapsed(s):25
...80 lines removed to reduce example size...
meters to dest:12790 M/s: 1000 time elapsed(s):107
meters to dest:11790 M/s: 1000 time elapsed(s):108
meters to dest:10790 M/s: 1000 time elapsed(s):109
meters to dest:9790 M/s: 1000 time elapsed(s):110
meters to dest:8791 M/s: 999 time elapsed(s):111
meters to dest:7793 M/s: 998 time elapsed(s):112
meters to dest:6796 M/s: 997 time elapsed(s):113
meters to dest:5800 M/s: 996 time elapsed(s):114
meters to dest:4805 M/s: 995 time elapsed(s):115
meters to dest:3811 M/s: 994 time elapsed(s):116
meters to dest:2818 M/s: 993 time elapsed(s):117
meters to dest:1826 M/s: 992 time elapsed(s):118
meters to dest:835 M/s: 991 time elapsed(s):119
meters to dest:-155 M/s: 990 time elapsed(s):120
you have arrived!
meters to dest:0 M/s: 0 time elapsed(s):1

CodePudding user response：

This should be fairly close to what you're looking for:

import time

meters = 10000
max_diatance = meters
distance = 0
traveling = True
meters_second = 0
max_meters_second = 90
seconds = 0

accelerating = True
accel_distance = 0

# can change interval here
seconds_per_intervul = 1

while traveling:
    # end travel
    if meters <= 0:
        traveling = False
        meters = 0
        meters_second = 0
        seconds = 0
        print('you have arrived!')
        break
    # if distance to de accelerate < max distance
    elif meters < accel_distance:
        meters_second -= 1

    # if crossed half way while still accelerating
    elif (distance > max_diatance/2) and (accelerating == True):
        accelerating = False
        accel_distance = distance

    # else if reached max speed
    elif meters_second >= max_meters_second:
        if accelerating == True:
            accel_distance = distance - meters_second * seconds_per_intervul
            accelerating = False
        # peak speed
        meters_second = max_meters_second

    # else keep accelerating
    else:
        meters_second =1


    # calc movement over interval
    distance  = meters_second * seconds_per_intervul
    meters -= meters_second * seconds_per_intervul
    seconds  = seconds_per_intervul
    print(f'dist to destination(m):{meters} M/s: {meters_second} time passed(s):{seconds}')
    time.sleep(seconds_per_intervul)

In this code I am assuming your goal is to reach a speed of 0 m/s at the same time you reach your destination as that falls within "realistic acceleration and deceleration". What this dose is track how far it took for the object to get to max speed, and then uses that distance to check when to stop accelerating. It also starts slowing down properly if it reached the half way point before reaching max speed.

Note that this still ends with some speed as it doesn't perfectly get the distance needed to deaccelerate because of both the large update interval, if you want prefect accuracy you are going to need to do math instead of just checking the relative distance every second. The formula is accel_diatance = max_meters_second**2 / (2*acceleration). You still can't stop exactly at 0 though because you would need to check the distance at an infinitely short interval to not miss the exact moment where you are at 0. For practical purposes you can either accept stopping with some amount of speed (like I did here), or you round the distance so you stop when when you are say within 0.1m and update significantly more frequently.

Accelerating for a hard coded length of time doesn't work if you want to use variable distances, and even then you have an issue in your implementation. Your code accelerates for 20 seconds, then jumps to the max speed of 10000m/s, which doesn't match your goal of realistic acceleration. Your code also doesn't slow down fast enough simply because the half way point is too short of a distance to deaccelerate from the max speed you set.

CodePudding user response：

I will suggest you another way i use in some animations.
Rather than changing speed over a constant time tic, i start from a constant speed but change the time tics to calculate position.
Let's see :
First sample code with a constant speed :

# A to B
meters = 100000 
# expected mean speed: 
meanSpeed = 10000 
# calculate expected duration 
expectedDuration = meters/meanSpeed # seconds for travel 
# now calculate each point
seconds = 0 
while (seconds < expectedDuration):
    elapsedTimeRatio = (seconds/expectedDuration)
    position = meters* elapsedTimeRatio
    print(elapsedTimeRatio, position)
    #Increment time
    seconds =0.1

Now notice that elapsedTimeRatio is a value between 0 and 1 .
It's a main advantage: if you use a non linear function that stays between 0 and 1, you can go from A to B in same time T, but the speed can change on the fly.
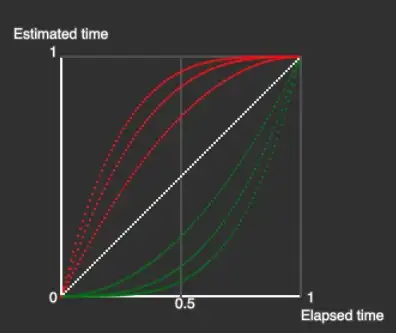
In the following picture, the white line is the travel at constant speed.
In green elapsedTimeRatio is transformed in estimatedTimeRatio by setting the first to power of 2, of 3, of 4 etc:

estimatedTimeRatio = elapsedTimeRatio **2 
position = meters* estimatedTimeRatio

You can see that the engine starts slowly ( when 0.5s of elapsed time has passed, the calculation of position uses estimatedTime which is very low ) then the curve accelerates to stay in time.
The red curves are the symetrics with the following functions

estimatedTimeRatio = 1- ( 1-elapsedTimeRatio)power of 2, 3, 4

In fact, you can use any function f(x) that stays between 0..1 when x stays between 0..1 (power, sin, cos, your function ,etc. )
Just try some.

HTH