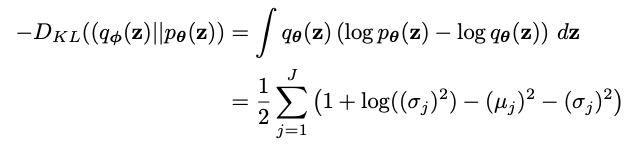KL Divergence loss Equation-CodePudding

I had a quick question regarding the KL divergence loss as while I'm researching I have seen numerous different implementations. The two most commmon are these two. However, while look at the mathematical equation, I'm not sure if mean should be included.

KL_loss = -0.5 * torch.sum(1   torch.log(sigma**2) - mean**2 - sigma**2)

OR 

KL_loss = -0.5 * torch.sum(1   torch.log(sigma**2) - mean**2 - sigma**2)
KL_loss = torch.mean(KL_loss)

Thank you!

CodePudding user response：

The equation being used here calculates the loss for a single example:

For batches of data, we need to calculate the loss over multiple examples.

Using our per example equation, we get multiple loss values, 1 per example. We need some way to reduce the per example loss calculations to a single scalar value. Most commonly, you want to take the mean over the batch. You'll see that most of pytorch's loss functions use reduction="mean". The advantage of taking the mean instead of the sum is that our loss becomes batch size invariant (i.e. doesn't scale with batch size).

From the stackoverflow post you linked with the implementations, you'll see the first and second linked implementations take the mean over the batch (i.e. divide by the batch size).

KLD = -0.5 * torch.sum(1   log_var - mean.pow(2) - log_var.exp())
...
(BCE   KLD) / x.size(0)

KL_loss = -0.5 * torch.sum(1   logv - mean.pow(2) - logv.exp())
...
(NLL_loss   KL_weight * KL_loss) / batch_size

The third linked implementation takes the mean over not just the batch, but also the sigma/mu vectors themselves:

0.5 * torch.mean(mean_sq   stddev_sq - torch.log(stddev_sq) - 1)

So instead of scaling the sum by 1/N where N is the batch size, you're scaling by 1/(NM) where M is the dimensionality of the mu and sigma vectors. In this case, your loss is both batch size and latent dimension size invariant. It's important to note that scaling your loss doesn't change the "shape" (i.e. optimal points stay fixed), it just scales it (which you can control how to step through via the learning rate).