I am trying to write a program about Simpson's Law.What I am trying to do is use as error as shown in this picture:
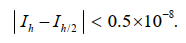 .
.
In the code i write the Ih is my f1 and Ih/2 is my f2.If the error doesnt happen then the steps get halved.
However I get this error
Traceback (most recent call last):
File "C:\Users\Egw\Desktop\Analysh\Askhsh1\example.py", line 22, in <module>
sim2 = simps(f2, x2)
File "C:\Users\Egw\Desktop\Analysh\Askhsh1\venv\lib\site-packages\scipy\integrate\_quadrature.py", line 436, in simps
return simpson(y, x=x, dx=dx, axis=axis, even=even)
File "C:\Users\Egw\Desktop\Analysh\Askhsh1\venv\lib\site-packages\scipy\integrate\_quadrature.py", line 542, in simpson
last_dx = x[slice1] - x[slice2]
IndexError: index -1 is out of bounds for axis 0 with size 0
Process finished with exit code 1
My code is
import numpy as np
from sympy import *
from scipy.integrate import simps
a = 0
b = np.pi * 2
N = 100
ra = 0.1 # ρα
R = 0.05
fa = 35 * (np.pi/180) # φα
za = 0.4
Q = 10**(-6)
k = 9 * 10**9
aa = sqrt(ra**2 R**2 za**2)
error = 5 * 10**(-9)
while True:
x1 = np.linspace(a, b, N)
f1 = 1 / ((aa ** 2 - 2 * ra * R * np.cos(x1 - fa)) ** (3 / 2))
sim1 = simps(f1, x1)
x2 = np.linspace(a, b, int(N/2))
f2 = 1 / ((aa ** 2 - 2 * ra * R * np.cos(x2 - fa)) ** (3 / 2))
sim2 = simps(f2, x2)
if abs(sim1 - sim2) < error:
break
else:
N = int(N/2)
print(sim1)
I wasnt expecting any error,and basically expecting to calculate correctly.
CodePudding user response:
When you reduce the grid step by half h -> h/2, the number of grid steps in turn grows N -> 2 * N, so you have to make two changes in your code:
- Define x2 to have twice as many elements as x1
x2 = np.linspace(a, b, 2 * N)
- Update N to be twice it was on the previous iteration
N = 2 * N
The resulting code would be
import numpy as np
from sympy import *
from scipy.integrate import simps
a = 0
b = np.pi * 2
N = 100
ra = 0.1 # ρα
R = 0.05
fa = 35 * (np.pi/180) # φα
za = 0.4
Q = 10**(-6)
k = 9 * 10**9
aa = sqrt(ra**2 R**2 za**2)
error = 5 * 10**(-9)
while True:
x1 = np.linspace(a, b, N)
f1 = 1 / ((aa ** 2 - 2 * ra * R * np.cos(x1 - fa)) ** (3 / 2))
sim1 = simps(f1, x1)
x2 = np.linspace(a, b, 2 * N)
f2 = 1 / ((aa ** 2 - 2 * ra * R * np.cos(x2 - fa)) ** (3 / 2))
sim2 = simps(f2, x2)
if abs(sim1 - sim2) < error:
break
else:
N = 2 * N
print(sim1)
And this prints the value
87.9765411043221
with error consistent with the threshold
abs(sim1 - sim2) = 4.66441463231604e-9
CodePudding user response:
@DmitriChubarov's solution is correct. However, your implementation is very inefficient: it does double the work it needs to. Also, simps is deprecated, you should be using proper exponential notation, and your function expression can be simplified. For an equivalent error-free algorithm that still doubles the input array length on each iteration but doesn't throw away the intermediate result,
import numpy as np
from scipy.integrate import simpson
a = 0
b = 2*np.pi
N = 100
ra = 0.1 # ρα
R = 0.05
fa = np.radians(35) # φα
za = 0.4
aa = np.linalg.norm((ra, R, za))
error = 5e-9
sim1 = np.nan
while True:
x = np.linspace(a, b, N)
f = (aa**2 - 2*ra*R*np.cos(x - fa))**-1.5
sim2 = simpson(f, x)
if np.abs(sim1 - sim2) < error:
break
sim1 = sim2
N *= 2
print(sim1)
CodePudding user response:
When I modified your code by adding two lines to print(len(x1), len(f1)) and print(len(x2), len(f2)), I got these results:
Output:
length of x1 and f1: 100 100
length of x2 and f2: 50 50
length of x1 and f1: 50 50
length of x2 and f2: 25 25
length of x1 and f1: 25 25
length of x2 and f2: 12 12
length of x1 and f1: 12 12
length of x2 and f2: 6 6
length of x1 and f1: 6 6
length of x2 and f2: 3 3
length of x1 and f1: 3 3
length of x2 and f2: 1 1
length of x1 and f1: 1 1
length of x2 and f2: 0 0
as you can see the length decreases each loop because N decreases and ends with an empty list length of x2 and f2: 0 0 and this causes the error you have had. To fix the issue of 'the empty list' I suggest that you duplicate N; this means using N*2 instead of N/2.
