How to compute local standard deviation efficiently-CodePudding

I need to compute the standard deviation in a neighborhood of a point for each point in a large (10M pixel) image. The end result should produce two results:

Get a feeling what is the standard deviation for sharp vs blurred images
Produce a mask for a new image that shows blurred and sharp areas of an image

At first, I've tried this approach, but it is very slow

b_arr, g_arr, r_arr = [], [], []
pad = 3

def compute_std(img, h, w):
    arr = [0, 0, 0]
    for c in range(len(arr)):
        arr[c] = np.std(img[h-pad:h pad 1, w-pad:w pad 1, c])
    return arr

img = cv2.imread('image_path.png')

for h in range(pad, img.shape[0] - pad):
    for w in range(pad, img.shape[1] - pad):
        b, g, r = compute_std(img, h, w)
        b_arr.append(b)
        g_arr.append(g)
        r_arr.append(r)

This approach takes minutes to produce the result. What is the right way to compute the standard deviations for each pixel of an image quickly?

Alternatively, is it faster to generate first several layers of a CNN, turn them to a vector for each point and then use some sort of a decision tree to classify a pixel as "sharp" or "blurred"?

CodePudding user response：

You can try to do it in the following way:

import skimage
img = cv2.imread('image_path.png')
pad = 3
c = 3
blks=skimage.util.view_as_windows(img,(pad,pad,c)) 
# get the image as blocks with shape (pad, pad, c)
blks = np.squeeze(blks) # squeeze the single dimension
# get std along height and width of each blk
std_view = blks.std(axis=(-3,-2))

CodePudding user response：

You can either use

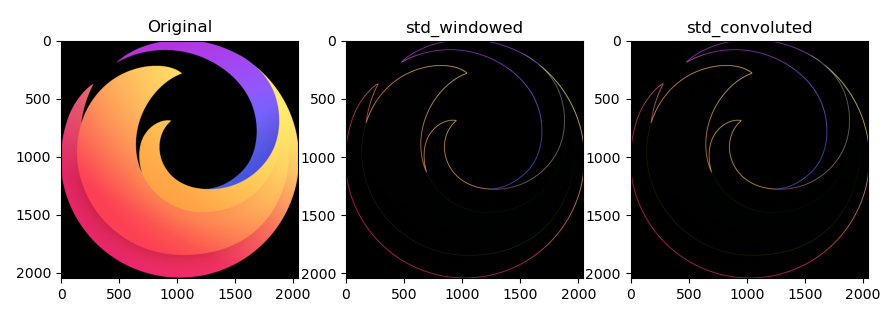
Complete code for reference:

from io import BytesIO

import matplotlib.pyplot as plt
import numpy as np
import requests
from numpy.lib.stride_tricks import sliding_window_view
from PIL import Image
from scipy.signal import convolve2d


def std_windowed(img, win_size):
    win_h, win_w = win_size
    win_view = sliding_window_view(img, (win_h, win_w), axis=(0, 1))
    return win_view.std(axis=(-2, -1))


def std_convoluted(img, win_size):
    img = np.moveaxis(img, -1, 0)  # HWC -> CHW
    img2 = img**2
    kernel = np.ones(win_size)
    kernel = kernel / kernel.size

    conv = lambda x: convolve2d(x, kernel, mode="valid")

    img_mean = np.stack([conv(band) for band in img], axis=-1)
    img2_mean = np.stack([conv(band) for band in img2], axis=-1)

    return np.sqrt(np.clip((img2_mean - img_mean**2), 0, None))


def get_image():
    url = "https://upload.wikimedia.org/wikipedia/commons/thumb/7/7a/Firefox_brand_logo,_2019.svg/2048px-Firefox_brand_logo,_2019.svg.png"
    response = requests.get(url)
    img = Image.open(BytesIO(response.content))
    return np.array(img)[..., :3].astype(float)


def minmax_scale(arr, *, vmin=0, vmax=1):
    amin, amax = arr.min(), arr.max()
    arr_std = (arr - amin) / (amax - amin)
    return arr_std * (vmax - vmin)   vmin


# Inputs
img = get_image()
win_size = 7, 7

# Compute both ways
std_win = std_windowed(img, win_size)
std_conv = std_convoluted(img, win_size)

# Maximum absolute error
print(np.abs(std_win - std_conv).max())

# Plot results
fig, (ax_orig, ax_std1, ax_std2) = plt.subplots(ncols=3)
ax_orig.set_title("Original")
ax_orig.imshow(minmax_scale(img))
ax_std1.set_title("std_windowed")
ax_std1.imshow(minmax_scale(std_win))
ax_std2.set_title("std_convoluted")
ax_std2.imshow(minmax_scale(std_conv))
plt.show()

# Performance
%timeit std_windowed(img, win_size)
%timeit std_convoluted(img, win_size)