plotting a boolean array as a translucent overlay over a graph with matplotlib-CodePudding

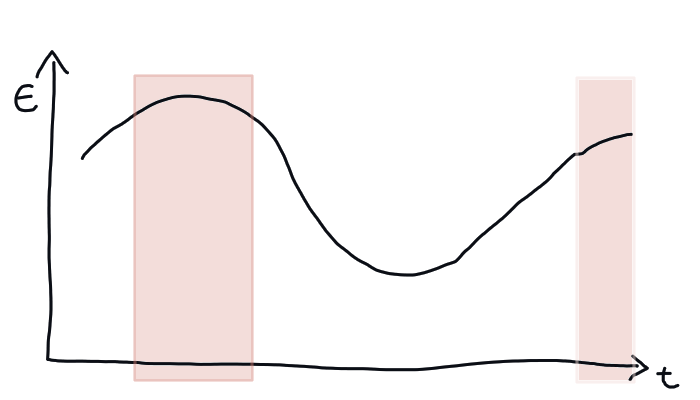
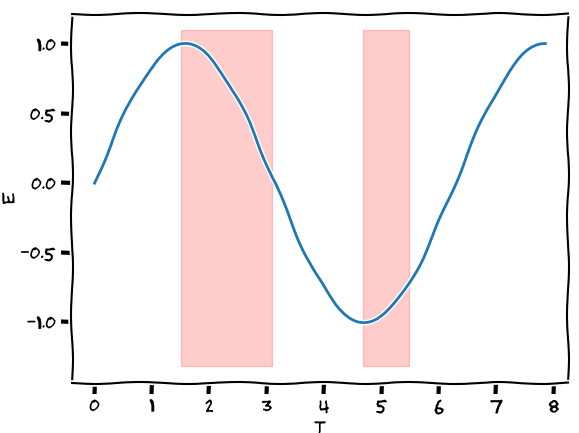
I want to plot the True parts of a boolean array as translucent boxes over another plot.

This sketch illustrates what I envision. I know I could do that with Asymptote, but I (among other reasons) need to verify that the data I work with is concise. I can supply example code of a graph and a boolean array if that helps - I don't have an idea yet how to realize the overlays, though. Asymptote might be the best option for producing plots for later publication, though.

CodePudding user response：

To overlay boxes, you can use

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.collections import PatchCollection
from matplotlib.patches import Rectangle

# boolean and plot data
n_points = 100
x = np.linspace(0, 2.5 * np.pi, n_points)
my_truth = np.zeros(n_points)
# true regions must be surrounded by false, pad by 1 false if needed
my_truth[20:40] = 1
my_truth[60:70] = 1


def get_truth_intervals(logical_data):
    """ extract 'true' regions embedded in 'false' regions """
    truth_spikes = np.diff(logical_data)
    truth_starts = np.argwhere(truth_spikes == 1)
    truth_ends = np.argwhere(truth_spikes == -1)
    return truth_starts, truth_ends


with plt.xkcd():
    fig = plt.figure()
    ax = plt.gca()
    ax.plot(x, np.sin(x))

    # draw boxes defined by true sections and plot height
    y_start, y_end = ax.get_ylim()
    boxes = [Rectangle((x[x_start[0]], y_start),
                       x[x_end[0]] - x[x_start[0]],
                       y_end - y_start)
             for x_start, x_end in zip(*get_truth_intervals(my_truth))]
    # implement all rectangles as a single collection
    pc = PatchCollection(boxes, facecolor="red", alpha=0.2,
                         edgecolor="red")
    ax.add_collection(pc)
    ax.plot()

plt.show()