How to calculate the distance of an object-CodePudding

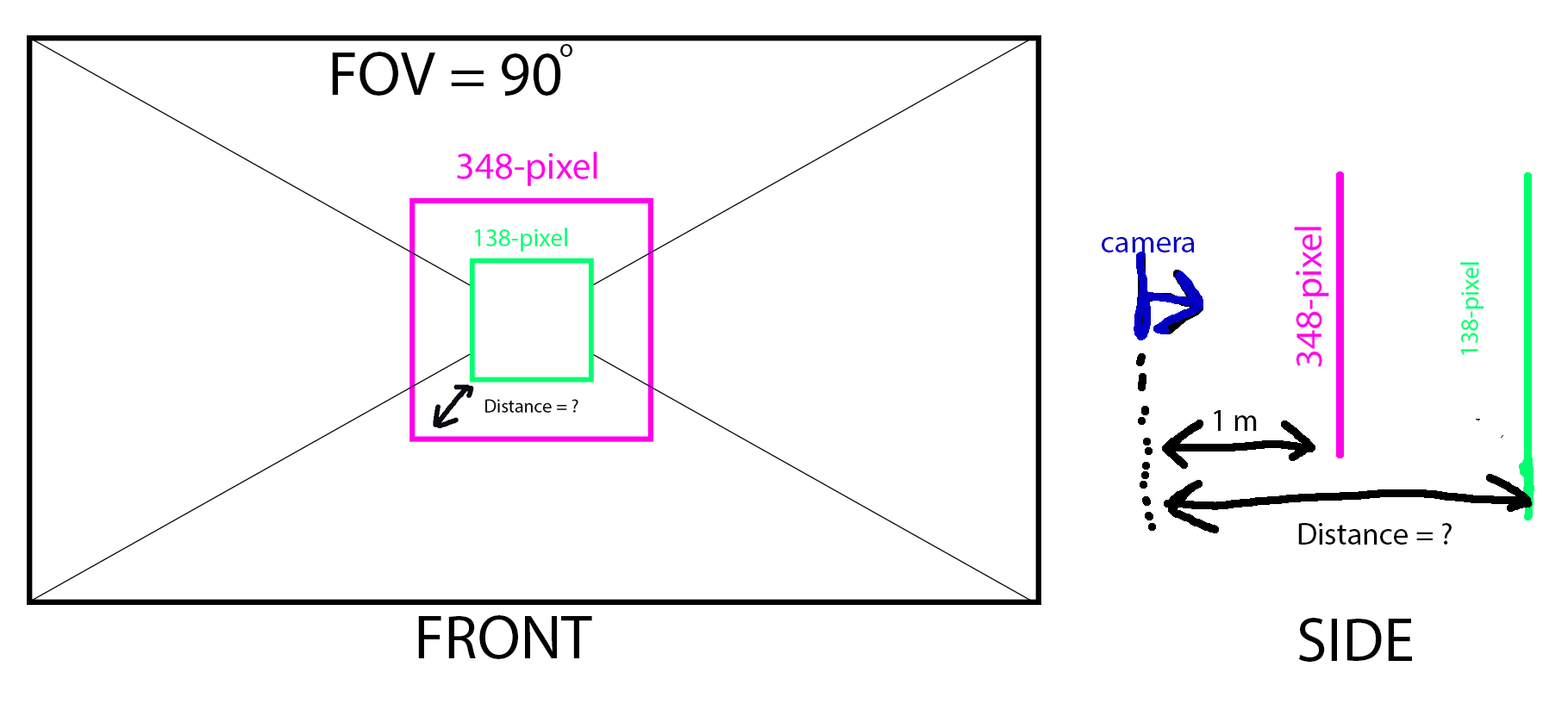
I have two screenshots (1920x1080) of a game, one with a 348-pixel-tall object that is 1 meter distant from the camera, and the other with a 138-pixel-tall version of the same thing. Given that the camera's field of vision is 90 degrees in the second screenshot, how can I precisely measure the object's distance from the camera?

I tried using a formula to determine the object's distance from the camera based on the object's height and camera distance, but the results were inaccurate.

CodePudding user response：

Precise answer: Without knowing the projection model, this is not possible.

An ad-hoc engineer's answer: One may assume the projection model is a pinhole camera model. This is probably a good assumption, because it is the model with least strange distortions and with geometrically beneficial properties. For a virtual game camera with horizontal* 90° opening angle this assumption seems to be reasonable.

Now you can translate your question into simple equations based on intercept and trigonometric theorems:

  (I)  w_1 / f = s / d_1
 (II)  w_2 / f = s / d_2
(III)  w_45 / f = tan(45°)

where
  f = focal length (unknown)
  s = object width (unknown)
  d_1 = object distance in image 1 = 1 m
  d_2 = object distance in image 2 (unknown)
  w_1 = object width in image coordinates in image 1 = 348 px
  w_2 = object width in image coordinates in image 2 = 138 px
  w_45 = 1920 px / 2

What remains is to solve this equation system:

(I) => f * s = w_1 * d_1
(II) => f * s = w_2 * d_2
___
=> w_1 * d_1 = w_2 * d_2
=> d_2 = w_1 * d_1 / w_2 = 348 px / (138 px) * 1 m = 2.52... m

So you do not even need equation (III). You would need it in case you are interested in focal length f = 960 px or object width s = 0.3625 m.

*I assume it is the horizontal opening angle from what is common and from what you drew in your question.

CodePudding user response：

This might be of interest. I don't think this approach is entirely accurate due to perspective distortions, but in this case, I think a fair estimate of Distance D from the camera can be obtained by assuming constant pixels-per-unit-angle near the centre of the picture. Assume the object are poles of height h and the camera is pointing at their centre. Suppose the angle from the centre of the camera view to the top of the pole at 1m is Theta_1 and for the other object it is Theta_2. Then

tan Theta_1 = h/2

tan Theta_2 = h/2D

(tan Theta_1) / (tan Theta_2) = D

Taking a first order approximation,

D approx1.= Theta_1 / Theta_2

If we also assume 348 Theta_2 = 138 Theta_1, then we get the answer posted. For a 2nd order approximation, which hopefully should be more accurate, particularly for more distended cases,...

D = (sin Theta_1)(cos Theta_2) / ((sin Theta_2)(cos Theta_1))

approx2.= Theta_1(1 - Theta_2^2/2) / (Theta_2(1 - Theta_1^2/2)) 

approx2.= (Theta_1/Theta_2)(1 - Theta_2^2/2)(1   Theta_1^2/2)

approx2.= (Theta_1/Theta_2)(1 - Theta_2^2/2   Theta_1^2/2)

So if 348 Theta_2 = 138 Theta_1

D approx2.= (348/138)(1   Theta_1^2(1/2 - (138/348)^2/2))

If 1920 pixels is pi/2 radians, then estimate

Theta_1 approx.= 348*pi/(2*2*1920) = 0.142353417

giving

D approx2.= (348/138)(1.008538919)

which suggests a less than 1 percent difference from the 1st order approximation in this case.