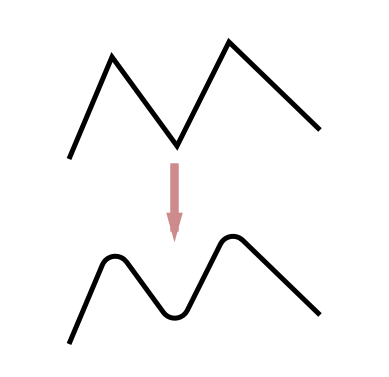
I am creating a drawing app in which I am using a custom interactable view, I am drawing an open path, I want its corners to be rounded. In android I can add cornerPathEffect but I am not able to do this in iOS
rounded corners of a path
CodePudding user response:
Many path-based drawing libraries have a path operator specifically designed to make drawing a rounded corner easier. UIBezierPath does not, but there is a version of addArc on both the lower-level 
The package is available in my RoundedPath repo on github. I will also paste the code here for posterity:
import CoreGraphics
/// One segment of a `CGPath`. A segment is an actual drawing command, not just a move command.
fileprivate enum Segment {
/// A straight line segment with the given start and end points.
case line(start: CGPoint, end: CGPoint)
/// A quadratic Bézier segment ending at the last given point.
case quad(CGPoint, end: CGPoint)
/// A cubic Bézier segment ending at the last given point.
case cubic(CGPoint, CGPoint, end: CGPoint)
var end: CGPoint {
switch self {
case .line(start: _, end: let end), .quad(_, let end), .cubic(_, _, let end):
return end
}
}
}
/// A complete subpath of a `CGPath`, with at least one segment and no moves or closePaths in the middle.
fileprivate struct Subpath {
/// The point at which `segments[0]` starts. Note that a `Segment` doesn't store its own start point.
var firstPoint: CGPoint
/// All my segments. Non-empty. If I'm closed, this ends with `.line(firstPoint)`.
var segments: [Segment] = []
/// True the subpath ended with .closeSubpath.
var isClosed: Bool = false
}
extension CGPath {
/// Create a copy of myself in which sharp corners are rounded.
///
/// - parameter radius: A radius to apply to sharp corners, which are corners between two straight-line segments. If a corner is an endpoint of a curve, it is not rounded.
/// - returns: A path in which each meeting of two straight-line segments has been rounded with a radius of `radius`, if possible. A smaller radius is used in corners where the line segments are too short to use the full `radius`.
public func copy(roundingCornersToRadius radius: CGFloat) -> CGPath {
guard radius > 0 else { return self }
let copy = CGMutablePath()
var currentSubpath: Subpath? = nil
var currentPoint = CGPoint.zero
func append(_ segment: Segment) {
switch currentSubpath {
case nil:
currentSubpath = .init(firstPoint: .zero, segments: [segment])
case .some(var subpath):
currentSubpath = nil
subpath.segments.append(segment)
currentSubpath = .some(subpath)
}
}
self.applyWithBlock {
let points = $0.pointee.points
switch $0.pointee.type {
case .moveToPoint:
if let currentSubpath, !currentSubpath.segments.isEmpty {
copy.append(currentSubpath, withCornerRadius: radius)
}
currentSubpath = .init(firstPoint: points[0])
currentPoint = points[0]
case .addLineToPoint:
append(.line(start: currentPoint, end: points[0]))
currentPoint = points[0]
case .addQuadCurveToPoint:
append(.quad(points[0], end: points[1]))
currentPoint = points[1]
case .addCurveToPoint:
append(.cubic(points[0], points[1], end: points[2]))
currentPoint = points[2]
case .closeSubpath:
if var currentSubpath {
currentSubpath.segments.append(.line(start: currentPoint, end: currentSubpath.firstPoint))
currentSubpath.isClosed = true
copy.append(currentSubpath, withCornerRadius: radius)
currentPoint = currentSubpath.firstPoint
}
currentSubpath = nil
@unknown default:
break
}
}
if let currentSubpath, !currentSubpath.segments.isEmpty {
copy.append(currentSubpath, withCornerRadius: radius)
}
return copy
}
}
extension CGMutablePath {
fileprivate func append(_ subpath: Subpath, withCornerRadius radius: CGFloat) {
var priorSegment: Optional<Segment>
// The overall strategy:
//
// - I don't draw the straight part of a line segment while processing the line segment itself.
// - When I process a line segment, if the prior segment was also a line, I draw the straight part of the prior segment and the rounded corner where the segments meet.
// - When I process a non-line segment, if the prior segment was a line, I draw the straight part of the prior segment.
//
// At each rounded corner, I clamp the radius such that the curve consumes no more than half of each segment.
if
subpath.isClosed,
case .line(start: let lastStart, end: let lastEnd) = subpath.segments.last!,
case .line(start: _, end: _) = subpath.segments.first!
{
// The subpath is closed, and the first and last segments are both lines. That means I need to round the corner between them when I process the first segment. I need to initialize currentPoint and priorSegment such that my normal line segment handling will draw the correct corner.
if subpath.segments.count < 3 {
// There are only one or two segments in this closed subpath. Since it's closed, there are two possibilities:
//
// - there is only one segment of zero length, or
// - the second (and last) segment is just the first segment with the endpoints reversed.
//
// Either way, the path cannot have a visible corner to be rounded, so I don't need to do any special initialization.
move(to: subpath.firstPoint)
priorSegment = nil
} else {
// There is indeed a roundable corner between the last and first segments. Since I'll clamp the radius to consume no more than half of each of those segments, the midpoint of the last segment is a safe value for currentPoint.
move(to: .midpoint(lastStart, lastEnd))
priorSegment = subpath.segments.last!
}
} else {
// It's not a closed subpath, or the first or last segment isn't a line, so there's no roundable corner at the start.
move(to: subpath.firstPoint)
priorSegment = nil
}
/// Call this when starting to process a non-line segment, to draw the straight part of priorSegment if needed.
func finishPriorLineIfNeeded() {
if
case .some(.line(start: _, end: let end)) = priorSegment,
end != currentPoint
{
addLine(to: end)
}
}
for currentSegment in subpath.segments {
// Invariants:
// - If priorSegment is nil, currentPoint is subpath.firstPoint.
// - If priorSegment is a line, currentPoint is somewhere on that segment, and priorSegment is only drawn up to currentPoint.
// - If priorSegment is non-nil and not a line, currentPoint is the end point of priorSegment and prior is fully drawn.
switch currentSegment {
case .line(start: let t1, end: let t2):
if case .some(.line(start: let t0, end: _)) = priorSegment {
// At least part of priorSegment is undrawn. This addArc draws any undrawn part of priorSegment, and draws the circular arc at the corner, but doesn't draw any of currentSegment after the arc. It leaves currentPoint at the endpoint of the arc, which is somewhere on currentSegment.
let cr = clampedRadius(
forCorner: t1,
priorTangent: .midpoint(t0, t1),
nextTangent: .midpoint(t1, t2),
proposedRadius: radius
)
addArc(tangent1End: t1, tangent2End: t2, radius: cr)
}
// I don't draw the rest of currentSegment here because some part of it may need to be replaced by an arc.
case .quad(let c, end: let end):
finishPriorLineIfNeeded()
addQuadCurve(to: end, control: c)
case .cubic(let c1, let c2, end: let end):
finishPriorLineIfNeeded()
addCurve(to: end, control1: c1, control2: c2)
}
priorSegment = currentSegment
}
if subpath.isClosed {
closeSubpath()
}
else if case .some(.line(start: _, end: let end)) = priorSegment, end != currentPoint {
addLine(to: end)
}
}
}
extension CGPoint {
fileprivate static func midpoint(_ p0: Self, _ p1: Self) -> Self {
return .init(x: 0.5 * p0.x 0.5 * p1.x, y: 0.5 * p0.y 0.5 * p1.y)
}
}
func clampedRadius(forCorner corner: CGPoint, priorTangent: CGPoint, nextTangent: CGPoint, proposedRadius: CGFloat) -> CGFloat {
guard
let transform = CGAffineTransform.standardizing(origin: corner, unit: priorTangent)
else { return 0 }
/// `transform` is a conformal transform that transforms `corner` to the origin and `priorTangent` to (1, 0), which is the construction required by `clamp(r:under:)`.
let scale = hypot(transform.a, transform.c)
let p = nextTangent.applying(transform)
let rScaled = proposedRadius * scale
let rScaledClamped = clamp(r: rScaled, under: p)
return rScaledClamped / scale
}
extension CGAffineTransform {
/// - parameter origin: A point to be transformed to `.zero`.
/// - parameter unit: A point to be transformed to `(1, 0)`.
/// - returns: The unique conformal transform that transforms `origin` to `.zero` and transforms `unit` to `(1, 0)`, if it exists.
fileprivate static func standardizing(origin: CGPoint, unit: CGPoint) -> Self? {
let v = CGPoint(x: unit.x - origin.x, y: unit.y - origin.y)
let q = v.x * v.x v.y * v.y
guard q != 0 else { return nil }
let a = v.x / q
let c = v.y / q
return Self(
a, -c,
c, a,
-(a * origin.x c * origin.y), c * origin.x - a * origin.y
)
}
}
/// Consider this construction:
///
/// p
/// ▞
/// ▞
/// ▞
/// ▞
/// ▞
/// ▞
/// ▞
/// ▞▚
/// ▞ ▚
/// ▞ ▚ c = (d, r)
/// ▞ ▌
/// ▞ ▌
/// ▞ ▌
/// ▞ ▌
/// ▟▄▄▄▄▄▄▄▄▄▄▙▄▄▄
/// 0 d (1,0)
///
/// `c` is distance `r` from the x axis and also distance `r` from the line to `p`. The coordinates of `c` are `(d, r)`.
///
/// I am given `p` and `r`, with `p.y ≠ 0`. Note that `p` could be less than 1 unit from the origin; it is not required to be far away as in the diagram.
///
/// My job is to compute `d`. If `abs(d)` is in the range 0 ... min(1, length(p), I return `r`. Otherwise, I compute the closest value to `r`
/// that would put `abs(d)` in the required range, and return that closest value.
fileprivate func clamp(r: CGFloat, under p: CGPoint) -> CGFloat {
// Since `r` is given,
let pLength = hypot(Double(p.x), Double(p.y))
/// Let theta be the angle between the x axis and vector `p`.
///
/// Therefore `c`, being equidistant from the x axis and the line through `p`, is at angle theta/2 from the x axis.
///
/// So `d` = `r` / tan theta/2.
///
/// Trig identity: tan theta/2 = (1 - cos theta) / sin theta.
///
/// cos theta = p.x / pLength
/// sin theta = p.y / pLength
/// tan theta/2 = (1 - cos theta) / sin theta
/// = (pLength - p.x) / p.y
///
/// d = r * p.y / (pLength - p.x)
///
/// Note that if `pLength == p.x`, `d` is undefined. But that only happens if `p.y == 0`, which violates my precondition.
let d = r * p.y / (pLength - p.x)
let dLimit = min(1, pLength)
if abs(d) <= dLimit { return r }
return abs(dLimit * (pLength - p.x) / p.y)
}
CodePudding user response:
There's no magic simple way. As you draw your path, you just need to use addArc(tangent1End...) at the appropriate moment(s).
CodePudding user response:
(Leaving this answer for future searchers who may need this, but see matt's answer for this question's specific situation.)
I assume you mean CGPath, not UPath (which does not exist). Line joins are applied to the CGContext prior to stroking the path.
cgContext.setLineJoin(.round)
If you use UIBezierPath, you can apply the line join style directly to the path:
path.lineJoinStyle = .round
