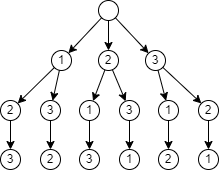
I have tasks and I want to calculate the most profitable order to arrange them.
Instead of checking every permutation and doing n*n! calculations, I want to build a tree of permutations, that is, the number of children at each level decreases by 1, and at each node the sub-permutation that has already been calculated will be saved and not recalculated.
For example, if I have 4 tasks, the tree will look like this:
My attached code is missing. I don't know how to build the tree and the give nodes the indexes as in the figure. I know how to deal with a binary tree, but not with a tree where the number of children is different at each lavel.
(The value of each task depends on its location. I know how to do that, so I didn't include it in the question).
int n = 4;
struct node
{
int task_index = -1;
double value;
struct node **next;
};
void build_tree(node *current_node, int current_level = 0)
{
if (current_level < 1 || current_level >= n)
return;
// current_node->task_index = ? ;
current_node->next = new node *[n - current_level];
for (int i = 0; i < n - current_level; i )
{
build_tree(current_node->next[i], current_level 1);
}
}
void print_tree(node *current_node, int current_level = 0)
{
// print indexes
}
void delete_tree(node *current_node, int current_level = 0)
{
// delete nodes
}
int main()
{
struct node *root = new node;
build_tree(root);
print_tree(root);
delete_tree(root);
delete root;
return 0;
}
CodePudding user response:
void build_tree(node *current_node, int current_level = 0)
{
if (current_level < 1 || current_level >= n)
return;
// current_node->task_index = ? ;
current_node->next = new node *[n - current_level];
for (int i = 0; i < n - current_level; i )
{
build_tree(current_node->next[i], current_level 1);
}
}
When called with the default parameter of current_level = 0, as you illustrate in your code below, this function exits on the first line without doing anything. You need to decide whether you are indexing starting from 0 or from 1.
Other than that, the general outline of the algorithm looks okay, although I did not explicitly check for correctness.
Now, more broadly: is this an exercise to see if you can write a tree structure, or are you trying to get the job done? In the latter case you probably want to use a prebuilt data structure like that in the boost graph library.
If it's an exercise in building a tree structure, is it specifically an exercise to see if you can write code dealing with raw pointers-to-pointers? If not, you should work with the correct C containers for the job. For instance you probably want to store the list of child nodes in a std::vector rather than have a pointer-to-pointer with the only way to tell how many child nodes exist being the depth of the node in the tree. (There may be some use case for such an extremely specialized structure if you are hyper-optimizing something for a very specific reason, but it doesn't look like that's what's going on here.)
CodePudding user response:
From your explanation what you are trying to build is a data structure that reuses sub-trees for common permutations:
012 -> X
210 -> X
such that X is only instantiated once. This, of course, is recursive, seeing as
01 -> Y
10 -> Y
Y2 -> X
If you look at it closely, there are 2^n such subtrees, because any prefix can have any one of the n input tasks used or not. This means you can represent the subtree as an index into an array of size 2^n, with a total footprint O(n*2^n), which improves on the vastly larger >n! tree:
struct Edge {
std::size_t task;
std::size_t sub;
};
struct Node {
std::vector<Edge> successor; // size in [0,n]
};
std::vector<Node> permutations; // size exactly 2^n
This will have this structure:
permutations: 0 1 2 3 4 ...
|-^
|---^
|-------^
|---^
|-^
Where the node at, e.g., location 3 has both task 0 and 1 already used and "points" to all (n-2) subtrees.
Of course, building this is not entirely trivial, but it compressed the search space and allows you re-use results for specific sub-trees.
You can build the table like this:
permutations.resize(1<<n);
for (std::size_t i = 0; i < size(permutations); i) {
permutations[i].successor.reserve(n); // maybe better heuristic?
for (std::size_t j = 0; j < n; j) {
if (((1<<j) & i) == 0) {
permutations[i].successor.push_back({j,(1<<j)|i});
}
}
}
CodePudding user response:
The recursive way to generate permutations is if you have n items then all of the permutations of the items are each of the n items concatenated with the permutations of the n-1 remaining items. In code this is easier to do if you pass around the collection of items.
Below I do it with an std::vector<int>. Once using a vector it makes more sense to just follow the "rule of zero" pattern and let the nodes have vectors of children and then not need to dynamically allocate anything manually:
#include <vector>
#include <algorithm>
#include <iostream>
struct node
{
int task_index = -1;
double value;
std::vector<node> next;
};
std::vector<int> remove_item(int item, const std::vector<int>& items) {
std::vector<int> output(items.size() - 1);
std::copy_if(items.begin(), items.end(), output.begin(),
[item](auto v) {return v != item; }
);
return output;
}
void build_tree(node& current_node, const std::vector<int>& tasks)
{
auto n = static_cast<int>(tasks.size());
for (auto curr_task : tasks) {
node child{ curr_task, 0.0, {} };
if (n > 1) {
build_tree(child, remove_item(curr_task, tasks));
}
current_node.next.emplace_back(std::move(child));
}
}
void print_tree(const node& current_node)
{
std::cout << "( " << current_node.task_index << " ";
for (const auto& child : current_node.next) {
print_tree(child);
}
std::cout << " )";
}
int main()
{
node root{ -1, 0.0, {} };
build_tree(root, { 1, 2, 3 });
print_tree(root);
return 0;
}