I know I must show some effort but I really have no idea how to solve this problem.
I know how to create circular masks: 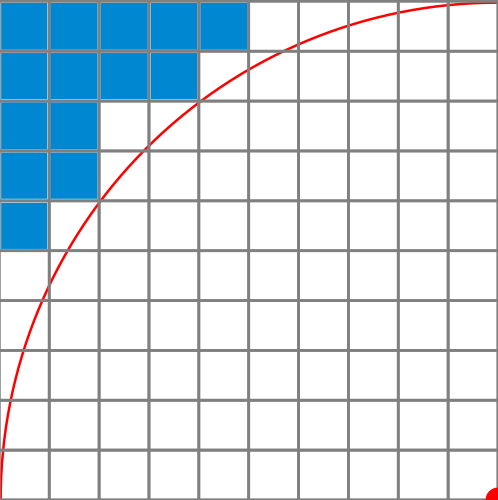
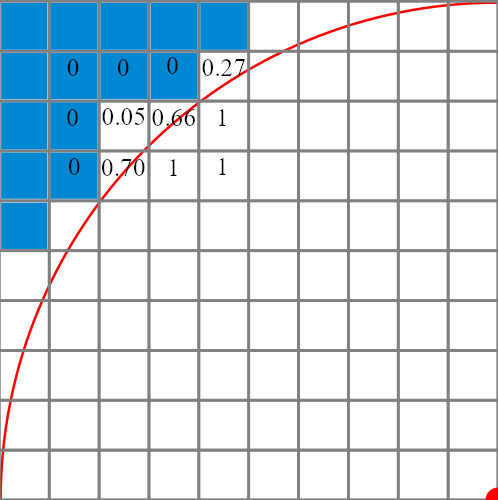
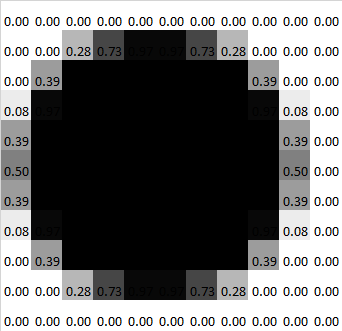
However I want to know how much of each pixel is under the circle. So basically I would have a float mask array and in the boundary of the circle I would have a value shows how much of the pixel is under the circle (percentage). Which I would like to call continuous.
Please note, the numbers given are not calculated and are eyeball estimate.
If anyone can point me to right direction I will be grateful.
CodePudding user response:
I suspect that there isn't an easy formula to give you the exact answer to this problem. If you needed to approximate, you could do something like the following:
Look at all for corners of a square:
- If all four corners are inside the circle, then the square is inside the circle
- If all four corners are outside the circle, then the square is outside the circle.
- Otherwise, divide the square into four equal subsquares and recurse
Recurse as deeply as need be to get whatever accuracy you need.
I hope someone has a better solution.
CodePudding user response:
Look online for a modified form of Xiaolin Wu's anti-aliasing line algorithm, which performs anti-aliasing for circle rendering.
While you are not doing any anti-aliasing here, you can easily use the alpha value this algorithm calculates as an ersatz measure of arc coverage over your set of pixels.
Note that you need only consider the subset of this set, over which the circle segment falls.
CodePudding user response:
If you are not after top accuracy, an easy measure is to compute the signed distance of the center of the pixel to the circle (which is the distance to the center minus the radius). Then if the distance is larger than 1, consider the pixel fully outside; if less than 0, fully inside. And of course in between, the distance tells you a fraction between 0 and 100%.
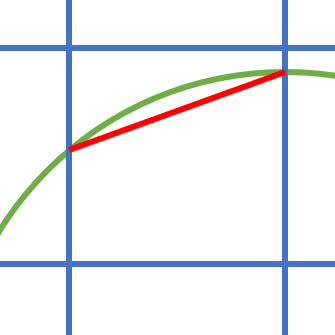
A more accurate technique is to compute that distance at the four corners of the pixel in order to find the two edges that are crossed (the sign changes between the endpoints). This allows you to construct a polygon (triangle, quadrilateral or pentagon, exceptionally hexagon when four sides are crossed) and compute its area by the shoelace formula. This is quite manageable.
For an exact result, you need to add the area of the circular segment between the oblique side of the polygon and the circle (