Linear regression in an array in python-CodePudding

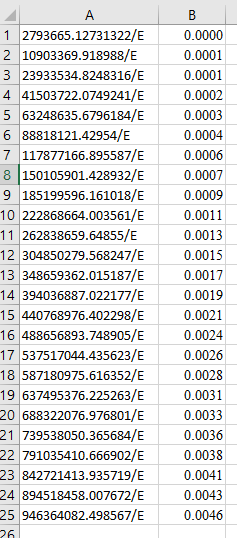
I have a one dimensional numpy array of symbolic equations and a one dimensional numpy array of values like this:

import numpy as np
import sympy as sp
E = sp.Symbol('E')

values = np.array([0.0, 0.0001, 0.0001, 0.0002, 0.0003, 0.0004, 0.0006, 0.0007, 0.0009, 0.0011, 0.0013, 0.0015, 0.0017, 0.0019, 0.0021, 0.0024, 0.0026, 0.0028, 0.0031, 0.0033, 0.0036, 0.0038, 0.0041, 0.0043, 0.0046])
equations = np.array([27405854.8989427/E, 106962058.905272/E, 234787976.631598/E, 407151513.555005/E, 620469116.017057/E, 871305771.223787/E, 1156375007.24571/E, 1472538893.01782/E, 1816808038.33958/E, 2186341593.87493/E, 2578447251.15228/E, 2990581242.5645/E, 3420348341.36898/E, 3865501861.68755/E, 4323943658.50655/E, 4793724127.67675/E, 5273042205.91346/E, 5760245370.79641/E, 6253829640.76983/E, 6752439575.14242/E, 7254868274.08736/E, 7760057378.64231/E, 8267097070.70941/E, 8775226073.05526/E, 9283831649.31095/E])

I am trying to find a single value of E that will give me the least amount of error with respect to each of the elements in the second array of values when substituted in the array of equations.

Can someone help?

Thank you.

CodePudding user response：

Scipy provides a method for minimizing a scalar function. So we just write an error function and let it do the rest.

values = np.array([0.0, 0.0001, 0.0001, 0.0002, 0.0003, 0.0004, 0.0006, 0.0007, 0.0009, 0.0011, 0.0013, 0.0015, 0.0017, 0.0019, 0.0021, 0.0024, 0.0026, 0.0028, 0.0031, 0.0033, 0.0036, 0.0038, 0.0041, 0.0043, 0.0046])
equations = np.array([2.74058549e 07, 1.06962059e 08, 2.34787977e 08, 4.07151514e 08,
       6.20469116e 08, 8.71305771e 08, 1.15637501e 09, 1.47253889e 09,
       1.81680804e 09, 2.18634159e 09, 2.57844725e 09, 2.99058124e 09,
       3.42034834e 09, 3.86550186e 09, 4.32394366e 09, 4.79372413e 09,
       5.27304221e 09, 5.76024537e 09, 6.25382964e 09, 6.75243958e 09,
       7.25486827e 09, 7.76005738e 09, 8.26709707e 09, 8.77522607e 09,
       9.28383165e 09])

def error(E):
    return np.mean(np.abs(equations/(np.abs(E) 10**(-20))-values))

minimize_scalar(error)

Notice that I wrote the function to avoid dividing by zero. The relevant values should be very large so the 10**-20 will not make a difference.

And it gives you x: 2018224283062.8733.

Btw. if you are happy with mean squared error instead of mean absolute error. (Other than the absolute value squaring keeps things differentiable.) You can do it with sympy too.

import numpy as np
import sympy as sp
E = sp.Symbol('E')

values = np.array([0.0, 0.0001, 0.0001, 0.0002, 0.0003, 0.0004, 0.0006, 0.0007, 0.0009, 0.0011, 0.0013, 0.0015, 0.0017, 0.0019, 0.0021, 0.0024, 0.0026, 0.0028, 0.0031, 0.0033, 0.0036, 0.0038, 0.0041, 0.0043, 0.0046])
equations = np.array([27405854.8989427/E, 106962058.905272/E, 234787976.631598/E, 407151513.555005/E, 620469116.017057/E, 871305771.223787/E, 1156375007.24571/E, 1472538893.01782/E, 1816808038.33958/E, 2186341593.87493/E, 2578447251.15228/E, 2990581242.5645/E, 3420348341.36898/E, 3865501861.68755/E, 4323943658.50655/E, 4793724127.67675/E, 5273042205.91346/E, 5760245370.79641/E, 6253829640.76983/E, 6752439575.14242/E, 7254868274.08736/E, 7760057378.64231/E, 8267097070.70941/E, 8775226073.05526/E, 9283831649.31095/E])

error = np.mean((equations-values)**2)
sp.solve(error.diff(E))

giving you

[2027858708334.55]

And a simple mathy argument would tell you that must be the global minimum. If you're interested in it I can add that.