How does this transparent extension come with a plot in lineplot?-CodePudding

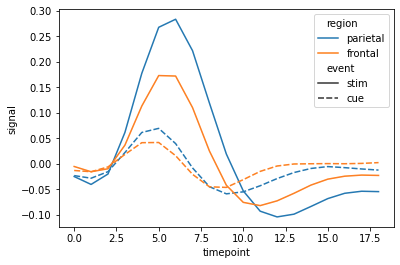
The plot in documentation looks like this : with code

sns.lineplot(x="timepoint", y="signal",
             hue="region", style="event",
             data=fmri)

and mine comes out to be like this 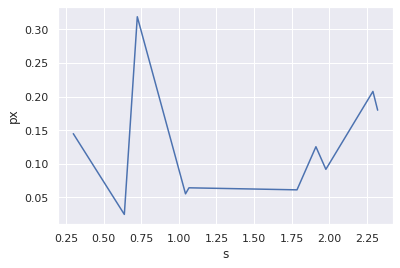for code :

sns.lineplot(
            # data=fmri, 
             x=df["_C_UP"]["s"][:10],
             y=df["_C_UP"]["px"][:10]
            #  hue="event"
             );

How do I get the same effect for those lines ( that transparent color around it )

here is what my data looks like

#Energy s   py  pz  px  dxy dyz dz2 dxz dx2 tot
50  -17.98094   0.72320 0.31781 0.00000 0.31882 0.0 0.0 0.0 0.0 0.0 1.35982
51  -17.87394   0.29726 0.14415 0.00000 0.14491 0.0 0.0 0.0 0.0 0.0 0.58632
52  -17.76794   0.63694 0.02456 0.00000 0.02484 0.0 0.0 0.0 0.0 0.0 0.68634
53  -17.66194   1.78595 0.06032 0.00001 0.06139 0.0 0.0 0.0 0.0 0.0 1.90766
54  -17.55494   1.97809 0.09038 0.00001 0.09192 0.0 0.0 0.0 0.0 0.0 2.16040

CodePudding user response：

It depends on the data. The plot from the seaborn documentation that you show is based on a dataset where for every x value there are several y values (repeated measurements). The lines in the plot then indicate the means of those y values, and the shaded regions indicate the associated 95% confidence intervals.

In your data, there is only one y value for each x value, so there is no way to calculate a confidence interval.

CodePudding user response：

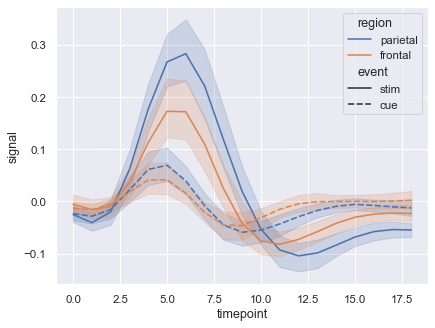
In the fmri datasets, there are actually multiple observations for each time point and subgroup, for example, at timepoint == 14 :

fmri[fmri['timepoint']==14]

    subject timepoint   event   region  signal
1   s5  14  stim    parietal    -0.080883
57  s13 14  stim    parietal    -0.033713
58  s12 14  stim    parietal    -0.068297
59  s11 14  stim    parietal    -0.114469
60  s10 14  stim    parietal    -0.052288
61  s9  14  stim    parietal    -0.130267

So the line you see, is actually the mean of all these observations (stratified by group) and the ribbon is the 95% confidence interval of this mean. For example, you can turn this off by doing:

sns.lineplot(x="timepoint", y="signal",
             hue="region", style="event",
             data=fmri,ci=None)

So to get the exact plot, you need to have multiple observations or replicates. If you don't, and your intention is to just connect the points, you cannot get a confidence interval.

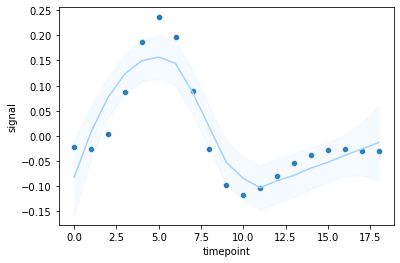
If you want to look at a trend line, one thing you can try is a polynomial smooth. And it makes sense to plot the data as points too.

Using an example from the same fmri dataset:

df = fmri[(fmri['subject']=="s5") & (fmri['event']== "stim") & (fmri['region'] == "frontal")]
sns.regplot(data=df,x = "timepoint",y = "signal",order=3)

Or use a loess smooth, which is more complicated (see