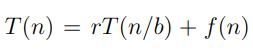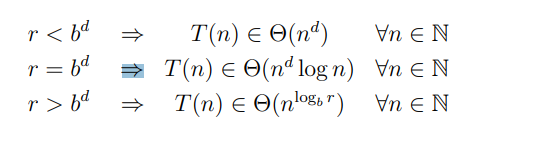After analyzing my algorithm, i found a recurrence:

T(n) = 2T(n/2)   log(n)

Is it possible to apply the master theorem for this form ?

If yes i am confused what the value of d would be in the theorem we saw in class :

I saw this post : Master's theorem with f(n)=log n but it didn't really help me to understand what the value of d would be if we have f(n) = logn

Thanks

CodePudding user response：

Using the notes from algorithmtutor, which gives the generic recurrence as T(n) = a T(n/b) f(n), this specific recurrence has a = b = 2, and the critical exponent is d = log_b a = log a / log b = 1. Since f(n) is O(log n), we know that f(n) is O(n^ε) for all ε > 0, in particular ε = 1/2, which is less than the critical exponent. This puts us squarely in Case 1 of the Master Theorem, which yields that T(n) = O(n^d) = O(n).